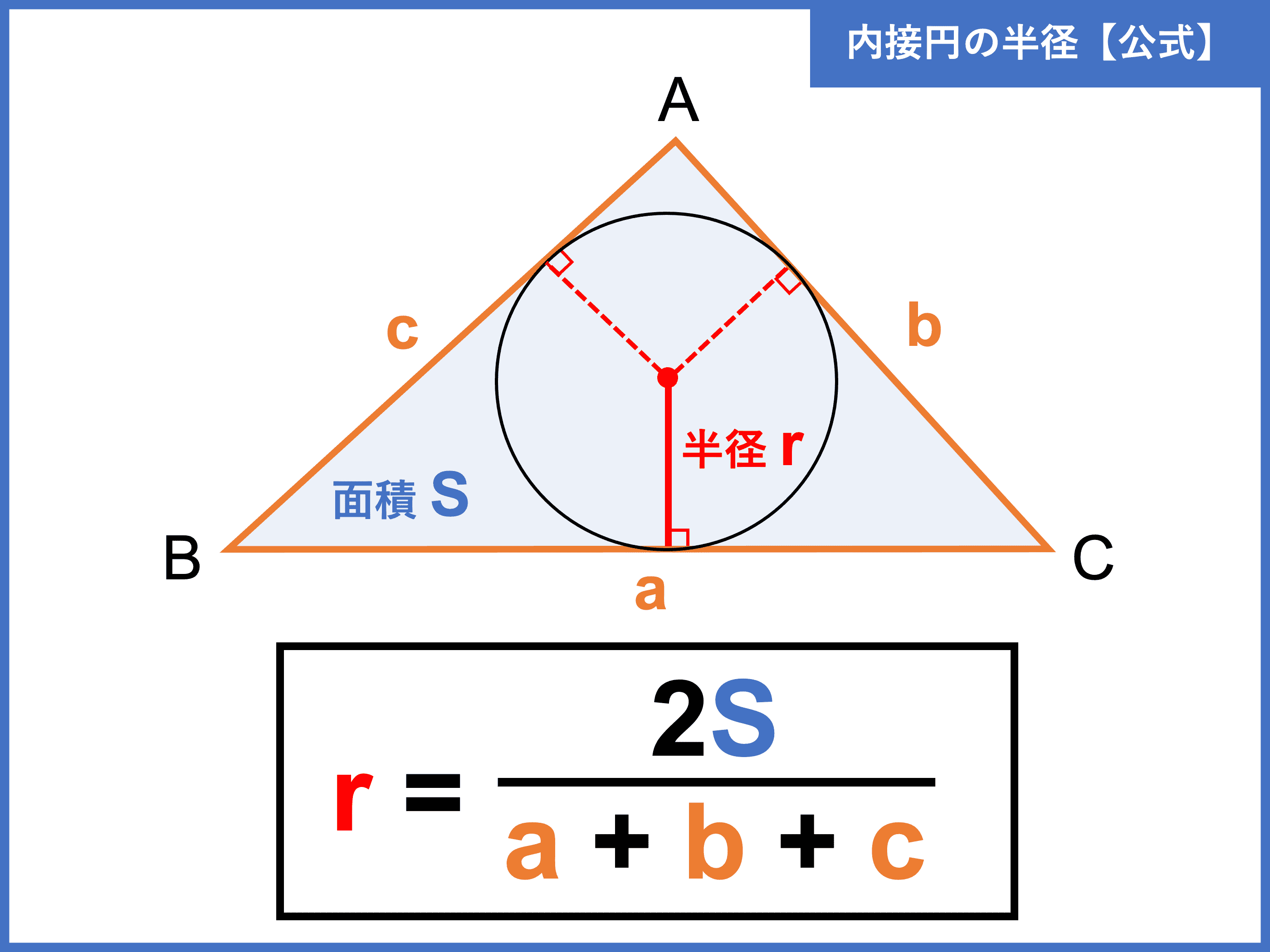
内接円の半径を計算する公式 内接円の半径 r r r を計算する問題では, S = r 2 (a b c) S=\dfrac{r}{2}(abc) S = 2 r (a b c) という公式を使います。 ただし, a, b, c a,b,c a, b, c は三角形の三辺の長さで, S S S は面積です。 さきほどの例題1を解いてみましょう。 単元 三角比, 「高校数学で扱う定理・公式等の確認,例題など。」, 学年 高校全学年, キーワード 内接円の半径 円の面積: πr2 π r 2 扇形の弧の長さ: 2πr× a 360 2 π r × a 360 扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さ: l l それぞれについて詳しく見ていき
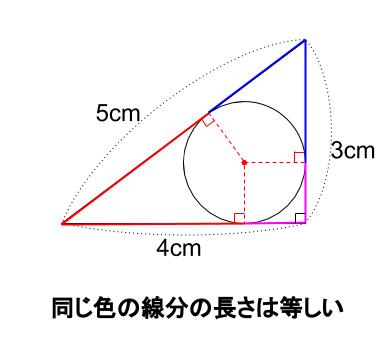
三角形の内接円 中学数学の無料オンライン学習サイトchu Su
円の半径の求め方 高校 公式
円の半径の求め方 高校 公式- は点 ( 2, 3) を中心とした半径 5 の円を表す方程式なのです。 つまり x 2 y 2 l x m y n = 0 ( l, m, n は整数) であれば 円の方程式 なのではないかと思われます。 もともと円であるとわかっている式を展開したらこのような形が出てきたのですから。 じゃあ逆にこれが円である証拠は・・・というと、 もちろん円の方程式に戻せるから です。 x 2 − 4 x y 2 − 6 x − 12 = 0 この式具体例で学ぶ数学 > 図形 > 円錐の母線、半径、中心角の関係式とそれぞれの求め方 最終更新日 r = l × x 360 という式を使うことで、 母線の長さ l 、 底面の半径 r 、 側面のおうぎ形の中心角 x のうち2つが分かれば残りの1つを計算できる。 なお
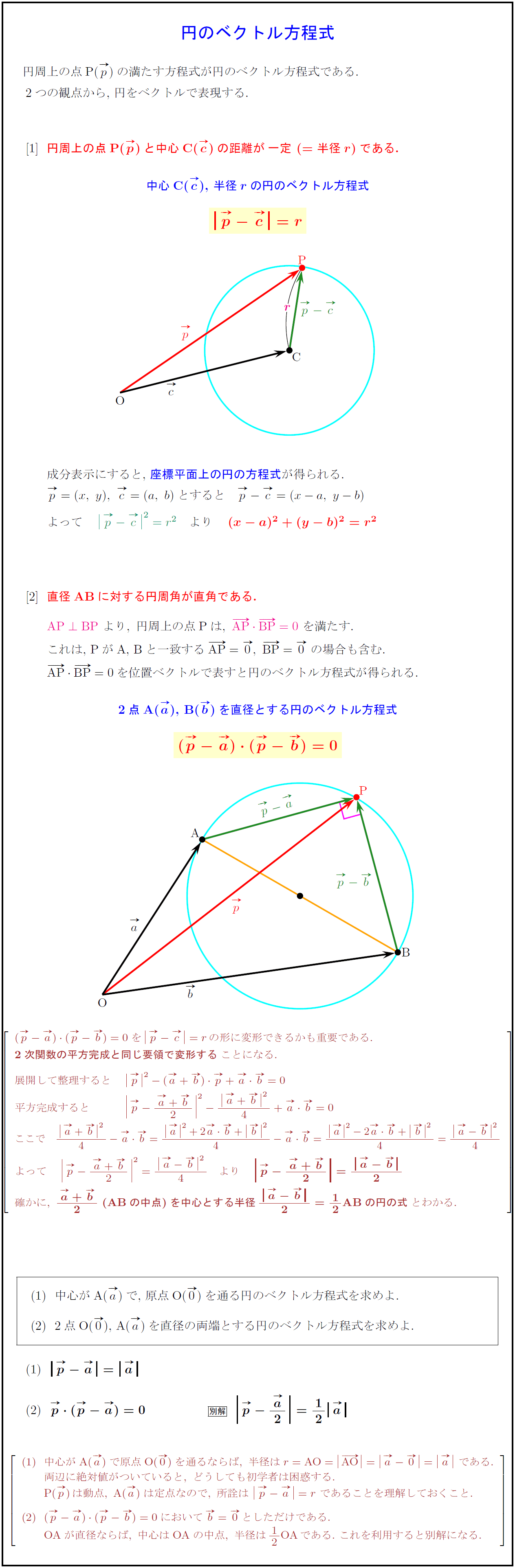



高校数学b 円のベクトル方程式2パターン 受験の月
について問題解説をしていくよ! 今回取り上げる問題はこちらだ! (1)中心が原点で、半径2の円 (2)中心 で、半径5の円 (3)中心 で、 軸に接する円 (4)中心 で、 軸に接する円 (5)中心 で、点 を通る円 (6)2点 、 を直径の両端とする円 (7 円の中心が点 、半径が の円の方程式は 特に、原点が中心 で、半径が の場合は 円の方程式の基本形は、「円の中心への距離が常に である」という条件を満たす点の集合、つまり 軌跡 といえます。 点 から距離が の位置にある点 について、三平方の定理より が常に成り立ちますね。 円の方程式(一般形)の公式 一方、円の方程式を一般形で表すと次のようになります。 円の方程式(一般 半径r㎝の円の、円周の求め方の公式の式教えてください 中学校 締切済 教えて!goo
外接円の半径と内接円の半径の関係 この式を整理して求める公式を得る。 「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。• 円の中心の座標や半径が「分かっているとき」は,円の方程式を(#1)の形で使うとよい.円の中心の座標や半径を「求めたいとき」は,(#1)の形に直せばよい. • 3点を通る円の方程式=三角形の外接円の方程式を求めたいときは,(#2)の形が使いやすい 弧長(円弧の長さ)L、弦長d、矢高(円弧の高さ)h、半径rのどれか2つに値を入力して、残りの2つを0と入力すると(空白にはしないでください)、その残りの2つおよび中心角を計算します。 L=r*θ, d=2*r*sin (θ/2), h=r* (1cos (θ/2))を用い、ニュートン・ラフソン
三角形の内接円の半径をrとおく 三角形を右図のように3つに分けると, と表せることが分かります S=rs となります 三角形の面積は,いろんな求め方がありますそこで, ヘロンの公式など を用いて三角形の面積を求めておくと,内接円の半径が求まり l = 2πr 「r」という文字が「円の半径」であることに注意してね。 直径は半径の2倍で「2r」になるんだ。 だから、 円周の長さ = 直径 × 円周率 っていう公式を「r」と「l」と「π」であらわしてやると、 ∠Aがわかってるので、BCの長さが求まれば外接円の半径が求められますね。 余弦定理より BC² = AB²+AC²-2×AB×AC×cosA = (2√2)²+3²-2×2√2×3×cos45° =8+9-12 = 5 ※2辺とその間の角から残りの辺の長さを求めるときにも余弦定理が使えました。 忘れてしまった人は、 余弦定理について解説した記事 をご覧ください。 BC>0より、 BC=√5 となります。 これでようやく



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ
高校の数学で内接円の半径が簡単に求められるのは S = r s の関係式です。 S= ab·sinC2nnnnnn から面積 S =6 √3√niが求められます。 余弦定理 c 2 =a 2 b 2 −2ab·cosC から c=7 → s = 72 nnnnn =9 が求められます。 これらを S=rs に代入すると 6 √3√ni =9r ⇒ r= 23n √3√ni (2) b=15,c=7,A=60° ? 高校の数学で内接円の半径が簡単に求められるのは S = r s の関係式です。X2 y2 2 ax 2 by a2 b2 r2 =0 となります。 これより,円の方程式は l,m,n を定数として, x2y2lxmyn=0・・・・・・ (2) (円の方程式は, (1)や (2)の形で表されます。 ) このように, 「2点間の距離」と「円の半径」が同じということを利用して,円の方程式を導く ことができます。 円の方程式の特徴は, ・ x2 と y2 の係数が等しい ・ xy の項を含まない という「 x と y の2次方 円の面積の求め方と覚えるコツ。 なぜ半径×半径×314になるか 円の面積は、 「半径 × 半径 × 314」 (半径 × 半径 × 円周率 π )という公式で求めることができます。 例題①半径 2 cmの円の面積を求めて下さい。 例題②半径 5 cmの円の面積を求めて下さい




高校入試数学 外接円の半径に関する対策問題 デルココ



2
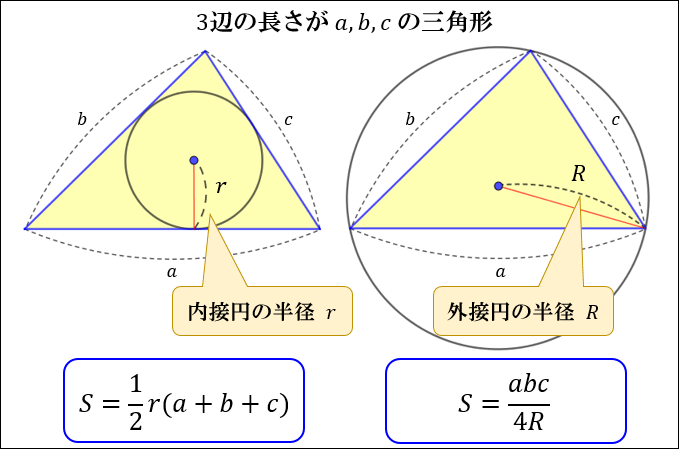
求めたい半径の大きさを ㎝とすると 半径が ㎝で中心角が1°の扇形の面積は と、表すことができます。 そして、面積が ㎠になるはずだから という二次方程式が完成します。 あとは、これを解いていけば の値(半径)を求めることができます。 この 内接円の半径r, ABCの面積Sとする S = 1 2 r(abc) ABCでa=, b=13, c=11である。 外接円の半径を求めよ。 内接円の半径を求めよ。 ① 余弦定理でcosAを出してからsinAを出して、正弦定理を利用する。 ② 三角形の面積を求めて、S = 1 2 r(abc)にあてはめる。 ① 余弦定理円外の点から円に接線を引くとき、左右対称な 2 2 本の接線が引けます。 どちらで解いても関係ないですね。 求める半径の長さを x x とすると 三平方の定理より x2 122 = 162 x 2 12 2 = 16 2 x2 144 = 256 x 2 144 = 256 x2 = 112 x 2 = 112 x = ±√112 x = ± 112 = ±4√7 = ± 4 7




扇形の弧の長さの求め方 公式と計算例




中学 数学 テクニック 三角形の外接円の半径の求め方 高校入試 高校受験 裏ワザ Youtube
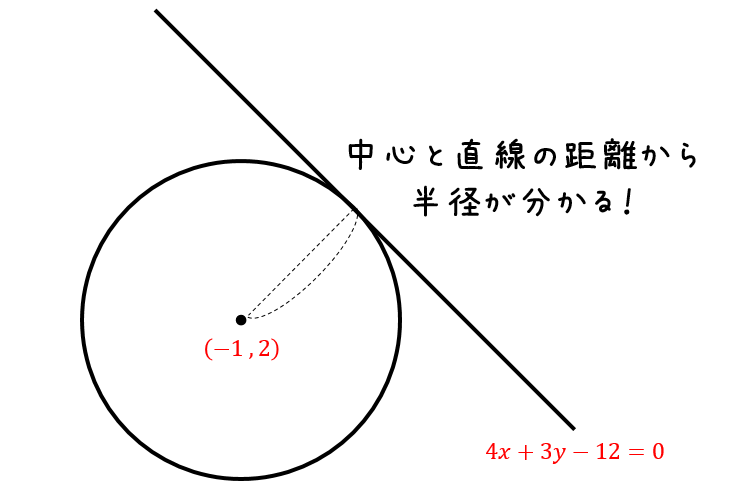
前回 https//wwwyoutubecom/watch?v=G4RJ4fV5k8&index=21&list=PLKRhhk0lEyzOfDE8u9U0GWX3aa43XeMOr 次回 https//wwwyoutubecom/watch?v=hfzt8TVzKBs&index 円の方程式の求め方をパターン別に解説 どんな問題であっても、問題文にある条件を公式に代入することで求められます。 では、そのパターンを例題とともに3つ確認してみましょう! まず、確認しておきたいのは円に関する情報の種類についてです 今回は小学校の算数で勉強する、円の面積・円周の求め方について書いていきたいと思います。(年6月日追記しました。) 円周の求め方公式 円の面積の求め方公式 円の面積・円周の長さを求める問題 問題① 《円の面積の求め方》 《円周の長さの求め方》 問題② 《円周
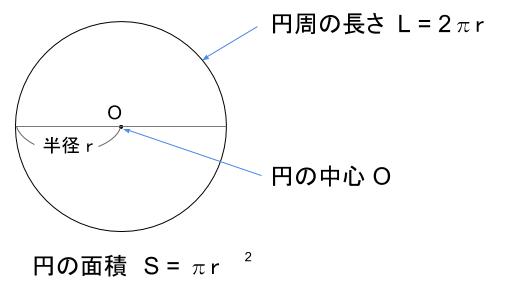



中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su
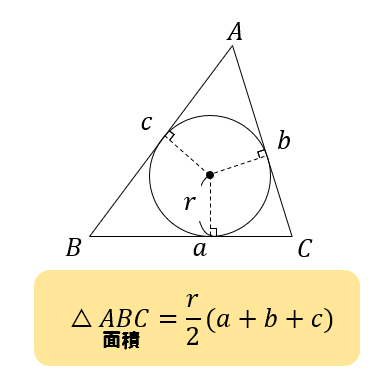



三角比 内接円の半径の求め方をイチから丁寧にやってみよう 数スタ
円の公式一覧 まとめ 円の公式 円周・面積 円周率 = 3.14 円周の長さ = 直径 × 円周率 円周率 = 円周 ÷ 直径 おうぎ形の弧の長さ = 直径 × 314 × 中心角 ÷ 360 円の面積 = 半径 × 半径 × 円周率 弧の面積 = 半径 × 半径 × 円周率 × 弧の角度 ÷ 360 円周の長さ 重要 円周率とは、「直径」を何倍したら「円周の長さ」になるかを表す数字です。 なので、 円周の長さ = 直径 × 円周率 となり円の半径を求める方法 円の半径とは、円の中心から円周上の任意の点を結んだ線の長さです。 半径を最も簡単に求める方法は直径を2で割ることです。直径がわからなくても、円周(C = 2\pi r )や円の面積(A = \pi r^{2} )など他の値が与えられている場合は、方程式を解いて半径(r)を求めることがここで、l は円周の長さ、π は円周率、d は円の直径、r は円の半径を表します。 小学生向けに、文字を使わずに書くと次のようになります。 (円周)= (直径)×(円周率)= 2×(半径)×(円周率) 円周を求めるには、この公式に円の直径 d または 円の



1



円の方程式
2つの方法で直径の両端が与えられた円の方程式を導出する。 円の中心と半径を求める ヒロ 今更であるが,直径の説明をしておく。 直径とは 円周上の2点を結ぶ線分(弦という)の中で,円の中心を通るものやその長さのことである。 考え方と解答 単元 円, 「リクエスト! 内接円の半径の求め方です! たぶん高校の範囲?だと思いますが、 中学生の方からリクエスト頂いたので 中学生対象で公開します! 中3の方には分かってもらえるように まとめたつもりです 求め方②の方がおすすめです 良かったら予習で見てください 先日の記事では詳しい外接円の半径の求め方は紹介していませんでしたが、 今回はそれについて紹介していきたいと思います! 高校数学であれば正弦定理などを用いるところですが、 "中学流" の求め方も是非活用してみてください!




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




Amazon Com Mathematics Formula For Difficult High School Passes Do You Answer In 10 Seconds Math Formula Japanese Edition Ebook Yoruhayonetaro Kindle Store
円の面積を求める公式は 円の面積 = 半径 × 半径 × 円周率 なので、半径を x とすると = x × x × 314 x × x = ÷ 314 x × x = 36 x = 6 ( c m) になります。 tweet share はてブ Pocket 三角形の外接円の半径を求める公式には、次の 種類があります。 公式① 正弦定理 外接円の半径の公式① の つの角 , , に向かい合う辺の長さをそれぞれ , , 、その外接円の半径を とすると、 正弦定理 より 正弦定理を変形しただけですね。 この公式を使うと、三角形の 辺の長さと、その辺に向かい合う角の大きさから外接円の半径を求められます。 合わせて読みたい 正弦定理とは? 公式や円の面積をだす公式は以下になります。 円の面積 = 半径 × 半径 × 314(円周率) このように 半径と円周率を利用することによって、円の面積を計算できます。 円の面積をだす公式は必ず覚えるようにしましょう。 円の面積から、円の半径を計算する なお半径を利用して円の面積をだすことができるというのは、円の面積を利用することによって円の半径を計算できることを意味しています。 半径



58 内接球の半径 Youtube




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
中学校では次のような公式を習うかと思います。 円の半径を r r 、同じく球の半径を r r とすると、 円の面積は A= \pi r^2 A = πr2 円周は \ell = 2\pi r ℓ = 2πr 球の体積は V=\frac {4} {3} \pi r^3 V = 34 πr3 球の表面積は S= 4\pi r^2 S = 4πr2 この式を見比べていて、中学生の時の僕は何か規則性があることに気づきました。 円の面積 A=\pi r^2 A = πr2 の式において、 r^2 r2 の 2 2 を前にか5年 学研教育情報資料センター 算数 学習相談 小/算数/5年/図形/ 正多角形と円/理解シート図形と方程式:円と直線 円の方程式(中心と半径) 説明 Date10年 5月10日 円の方程式について考えていきます。 円は中心からの距離となる半径が一定である点の集まりなので, 中心の点を ,半径を ,円周上の点を とすると , 三平方の定理より, が



内接円の半径




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
円の面積と円周の求め方(公式) 続いて、円の面積と円周の長さを求める公式をご紹介します。 円の面積と半径 円の面積 (S) = 半径 (r) 2 × 円周率 (π) 円周の長さと直径 円周の長さ (L) = 直径 (R) × 円周率 (π) 円の面積と円周の長さ 円の面積 (S) = 円周の長さ (L) × 半径 (r) ÷ 2 円の面積 (S) = 円周の長さ (L) 2 ÷ 円周率 (π) ÷ 4 著者 やまでら くみこ円の中心と半径を求めるためには、平方完成して式変形する! ということでしたね。 手順を覚えてしまえば簡単です(^^) それでは、解き方の手順を身につけたところでもう1問だけ解説しておきます。 そ




3分で分かる 三角形の外接円の半径の長さの求め方をわかりやすく 合格サプリ



円の方程式の公式や求め方をわかりやすく解説 円の接線も 受験辞典
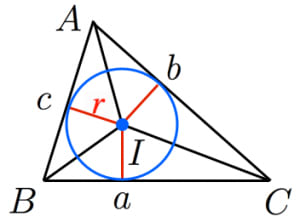



内接円の半径と三角形の面積 高校数学の美しい物語




高校数学 内接円の半径の求め方 例題編 映像授業のtry It トライイット




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ
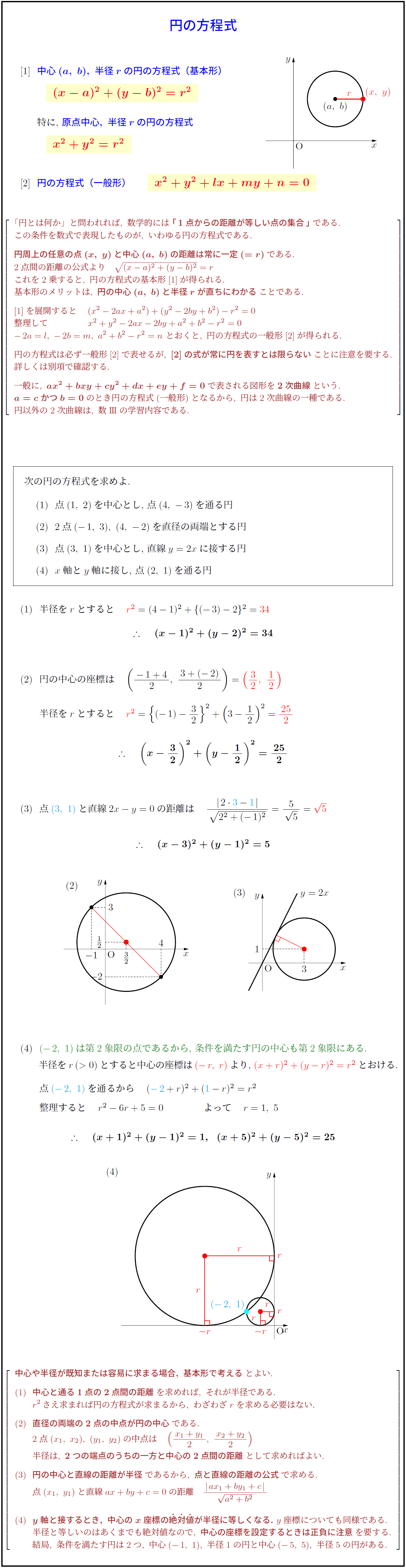



高校数学 円の方程式の基本形と一般形 座標軸と接する円 受験の月
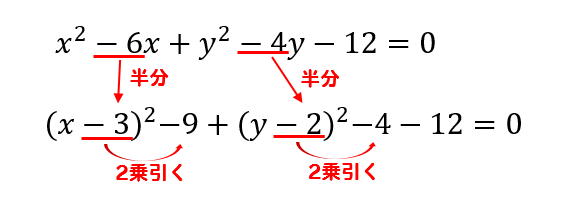



円の方程式 中心の座標と半径の求め方を解説 数スタ



内接円とは 半径の公式や求め方 性質をわかりやすく解説 受験辞典



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




高校入試file 002 数学 平面図形 難問 内接円の半径の求め方 相似形を見つける Youtube




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ




高校数学b 円のベクトル方程式2パターン 受験の月
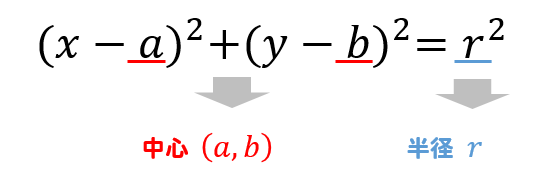



円の方程式 中心の座標と半径の求め方を解説 数スタ




Tikz 数学 三角形の内接円の半径の求め方 数樂管理人のブログ




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




円の面積の公式 算数の公式




高校数学 円に内接する四角形の計量 基本と裏技のまとめ トレミーの定理 ブラーマグプタの公式他 受験の月




円の面積の求め方を考えよう 小学校6年生の算数教材から 身勝手な主張




円 扇形 の面積 周や弧の長さの公式 数学fun




高校 数学 三角比33 内接円の半径 14分 Youtube




高校数学 正弦定理と外接円 例題編 映像授業のtry It トライイット



3




高校数学 内接円の半径の求め方 例題編 映像授業のtry It トライイット




なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル




高校数学 円と直線の位置関係の分類 映像授業のtry It トライイット




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ



円の方程式の求め方まとめ パターン別に解説するよ 数スタ



Tikz 数学 三角形の内接円の半径の求め方 数樂管理人のブログ




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト




Download 高校数学 A 演習 三角 Images For Free



3




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




三角形の内接円 中学数学の無料オンライン学習サイトchu Su




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




円周の求め方 公式と計算例
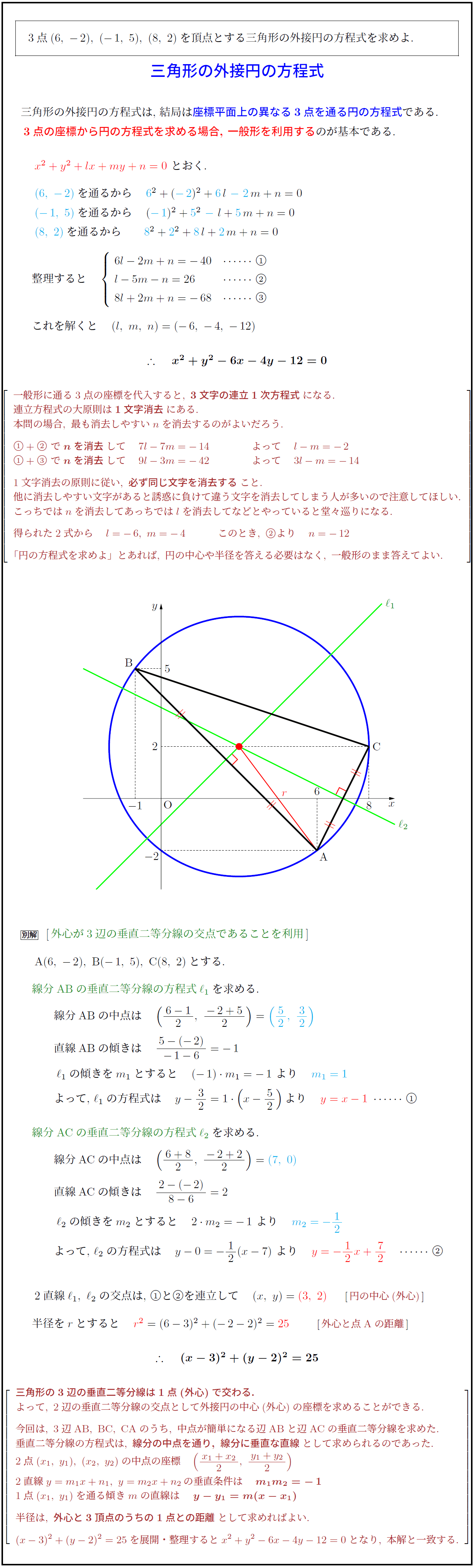



高校数学 三角形の外接円の方程式 受験の月



円の方程式の公式や求め方をわかりやすく解説 円の接線も 受験辞典




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ




内接球の半径を求める公式と例題 証明 高校数学の美しい物語
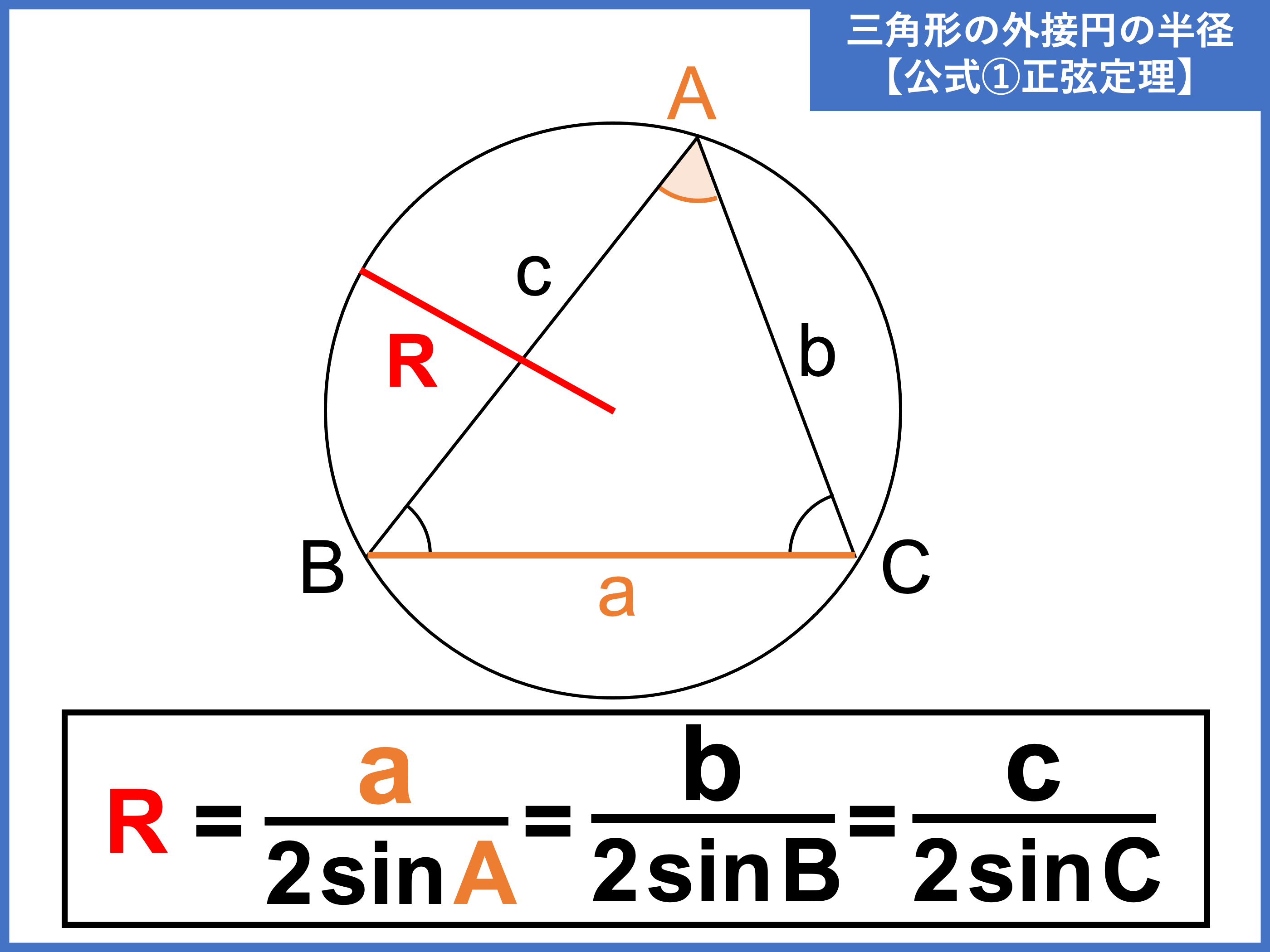



外接円とは 半径の公式や求め方 性質をわかりやすく解説 受験辞典
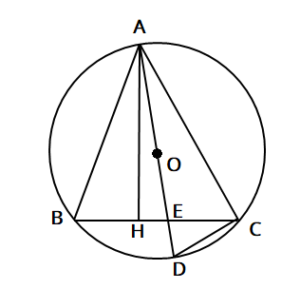



高校入試数学 外接円の半径に関する対策問題 デルココ
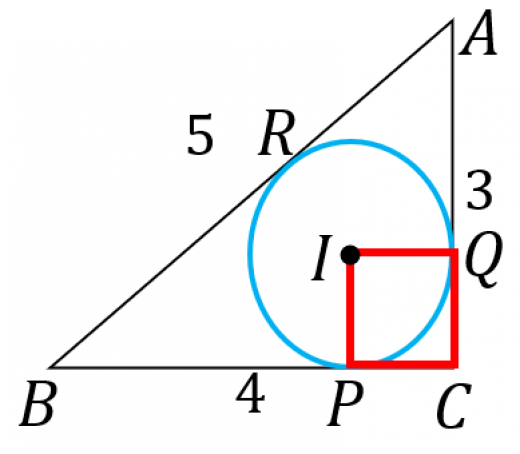



内接円の半径と三角形の面積 高校数学の美しい物語
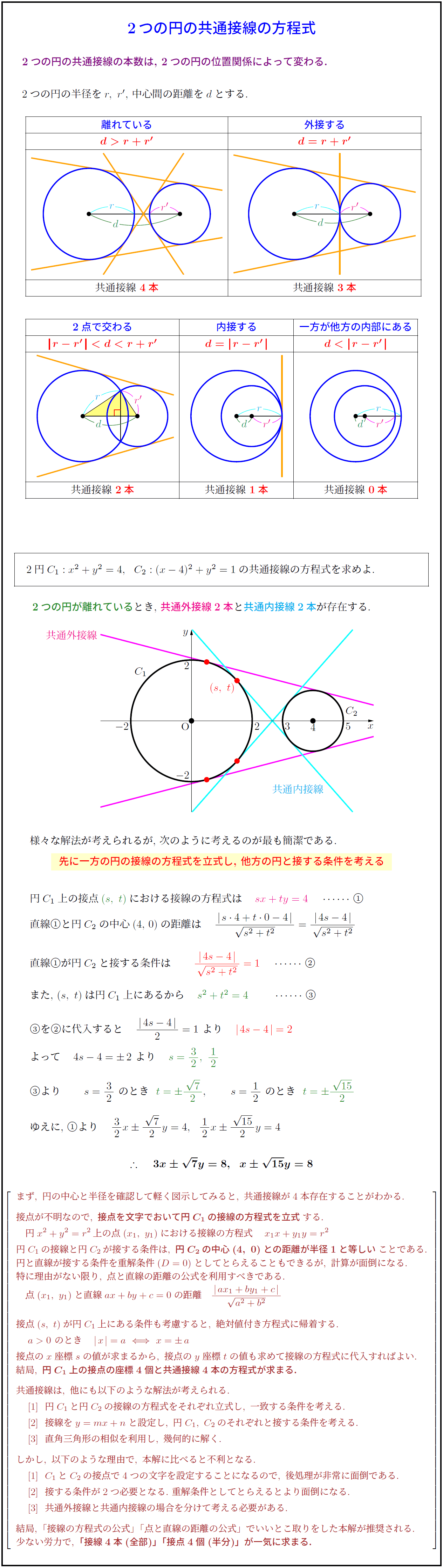



高校数学 2つの円の共通接線の方程式 受験の月
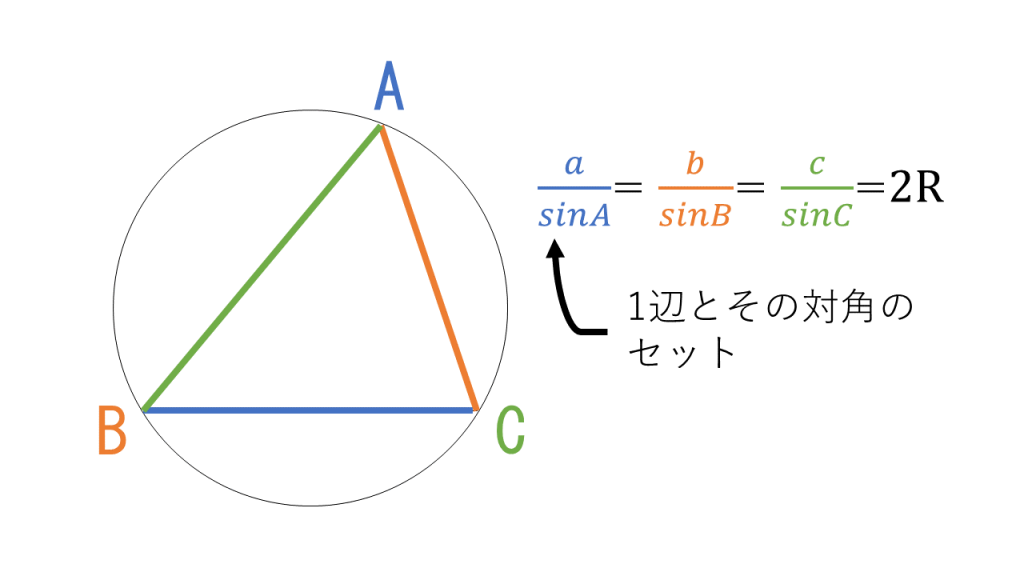



3分で分かる 三角形の外接円の半径の長さの求め方をわかりやすく 合格サプリ




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
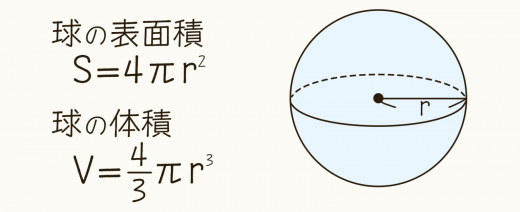



球の体積と表面積の公式の覚え方 積分での求め方 高校数学の美しい物語




数学 外接円の半径 高校入試 正解 名古屋市西区の高校生 中学生向け進学個別指導塾 名学館庄内通校
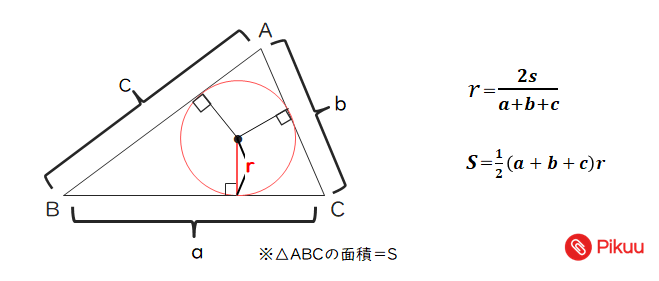



高校入試対策数学 三角形に内接する円の半径の長さを求める Pikuu



円の方程式と半径の関係は 1分でわかる意味と関係 求め方 公式と変形式




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




数学 外接円の半径 高校入試 正解 名古屋市西区の高校生 中学生向け進学個別指導塾 名学館庄内通校




高校数学 円と直線の位置関係 受験の月




高校数学 三角形の外接円の半径 内接円の半径と面積の関係 S 1 2r A B C 受験の月




高校数学 内接円の半径の求め方 例題編 映像授業のtry It トライイット
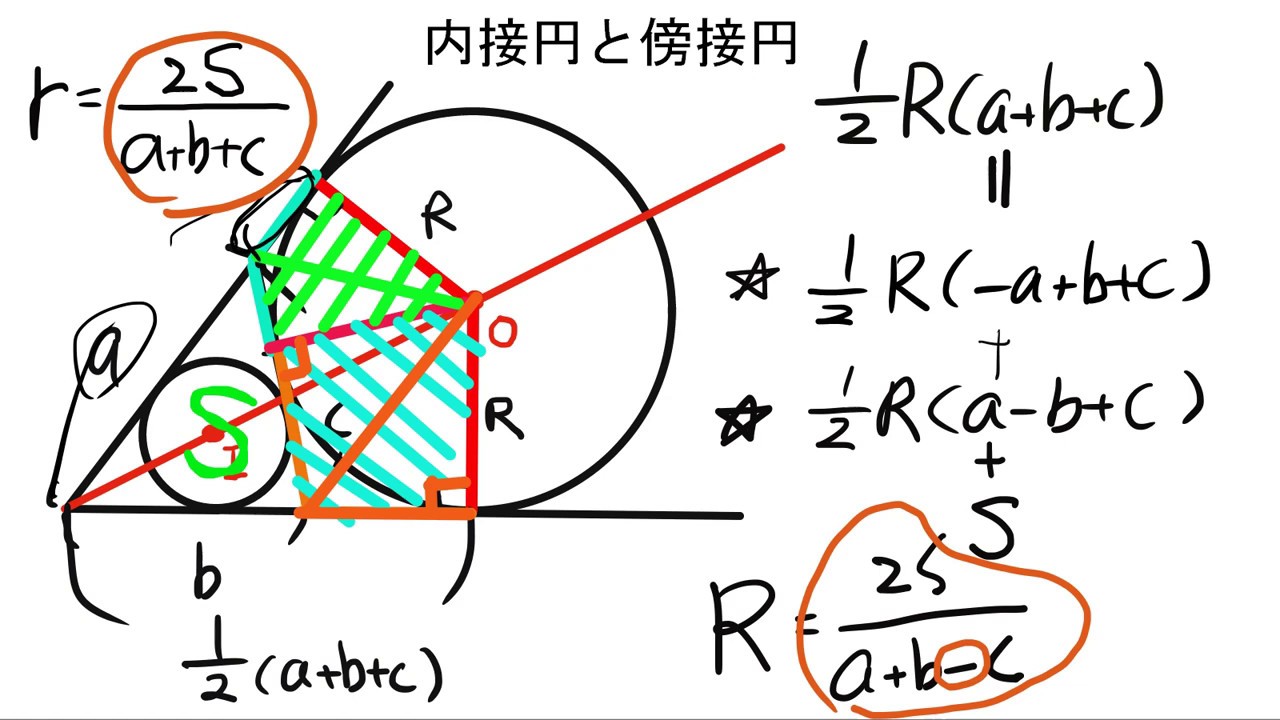



内接円と傍接円の半径公式 Youtube




高校数学 数 97 内接円と外接円の半径 Youtube
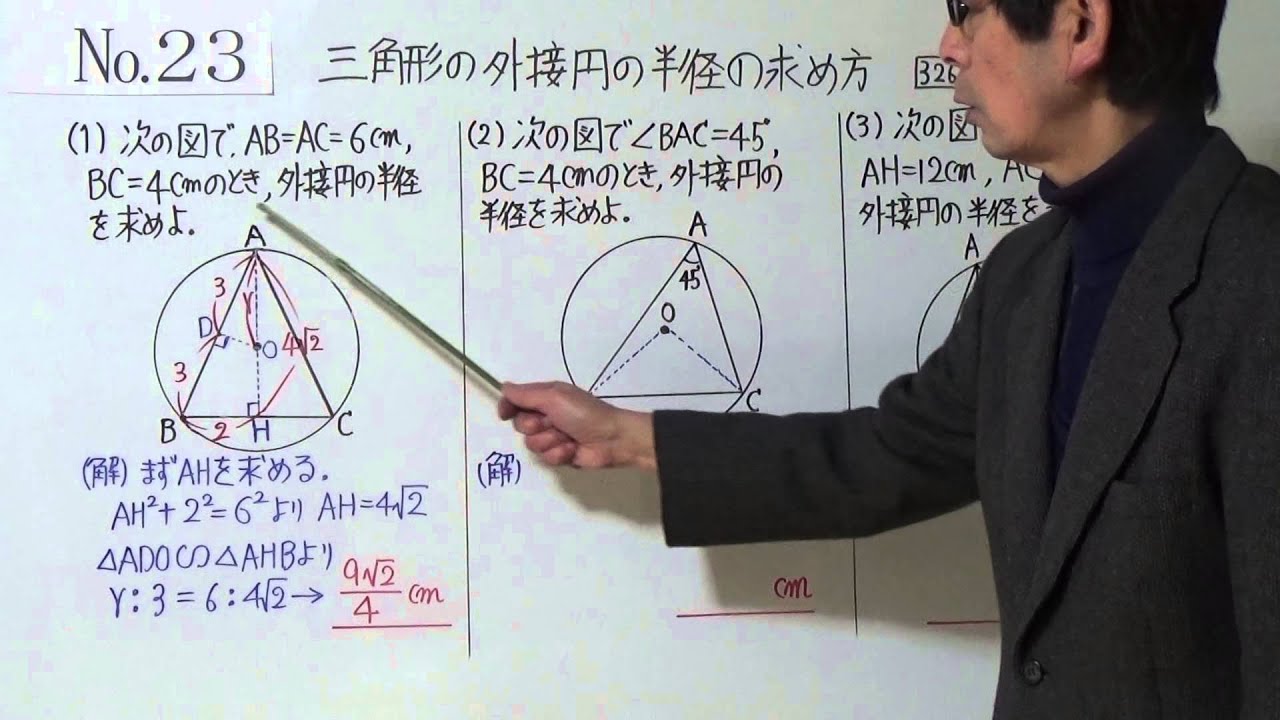



中3 23 4三角形の外接円の半径 Youtube




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト




高校入試対策数学 円錐に関する対策問題 Pikuu




円の面積の求め方 公式と計算例
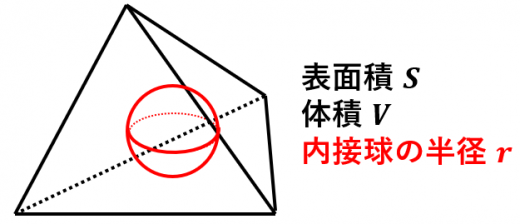



内接球の半径を求める公式と例題 証明 高校数学の美しい物語




円の方程式の求め方まとめ パターン別に解説するよ 数スタ




高校数学 内接円の半径の求め方 例題編 映像授業のtry It トライイット




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく
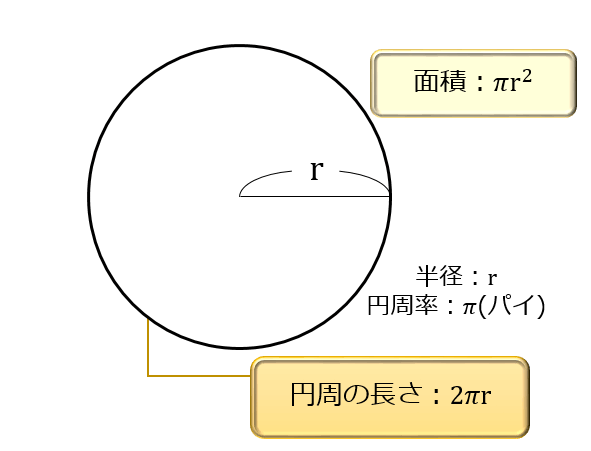



円周の求め方 円周率とは何か なぜ無限に続くのかを説明 その割り切れない理由について アタリマエ
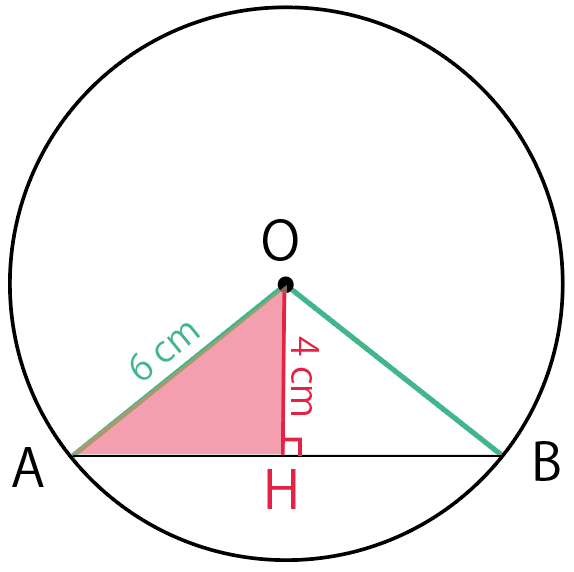



中3数学 弦の長さを求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
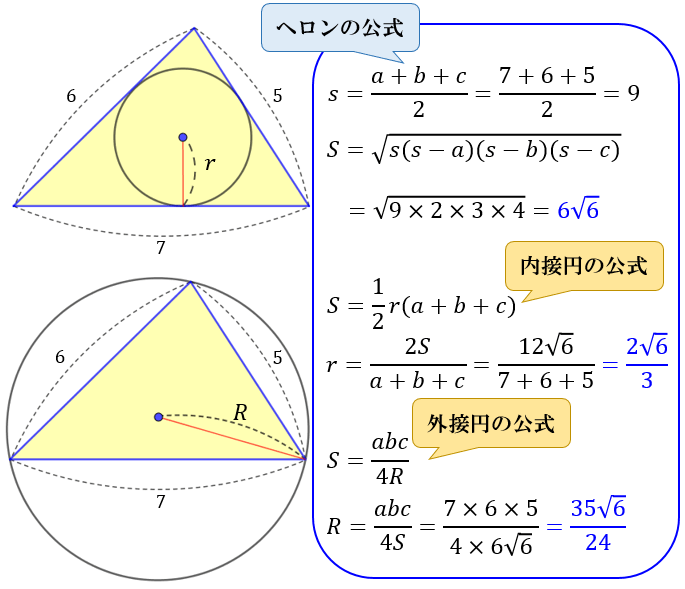



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
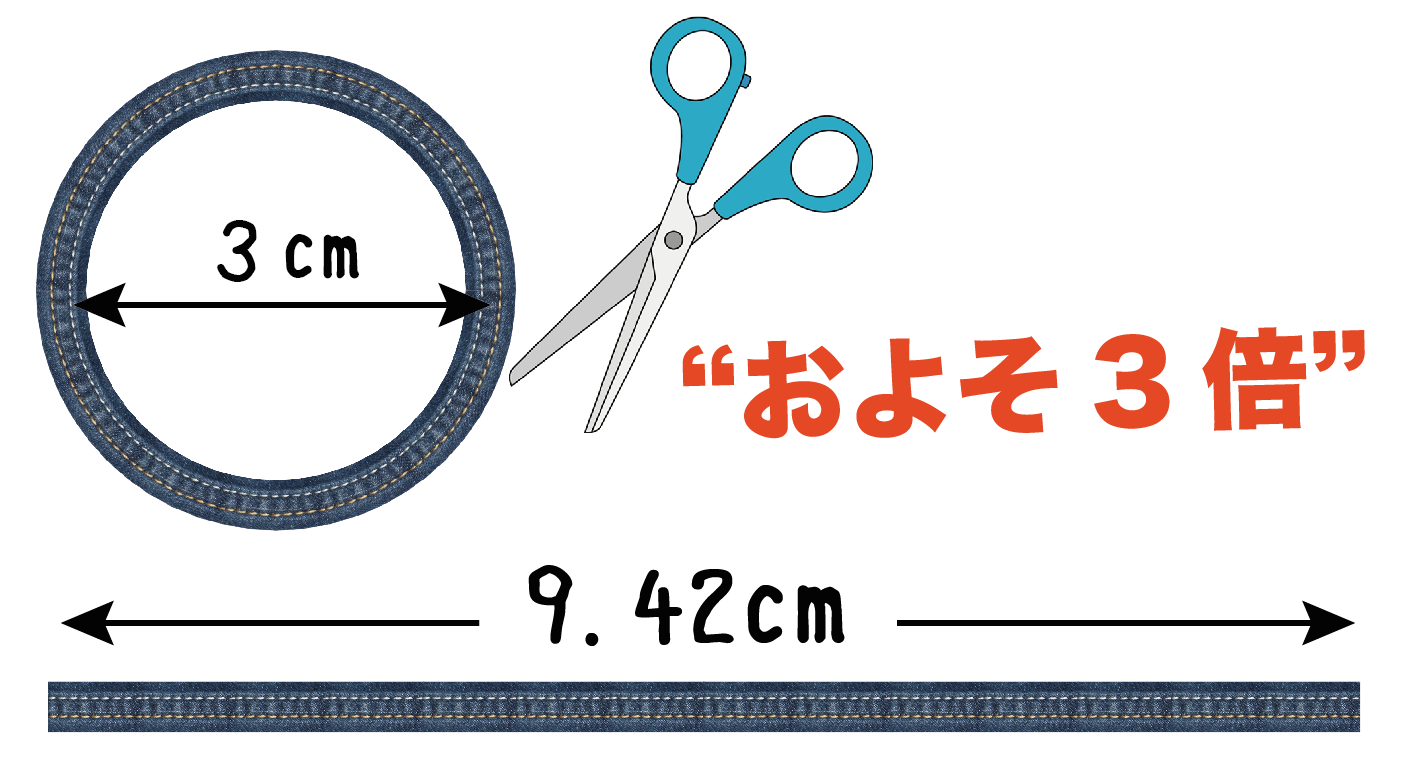



直径から計算 円周の長さの求め方 の公式を3秒で覚える方法 Qikeru 学びを楽しくわかりやすく
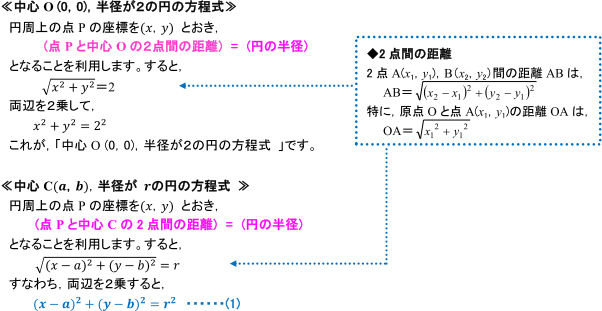



円の方程式の導き方 数学 苦手解決q A 進研ゼミ高校講座




三角形の面積を外接円の半径を使って求める Schoolmath S Diary




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ
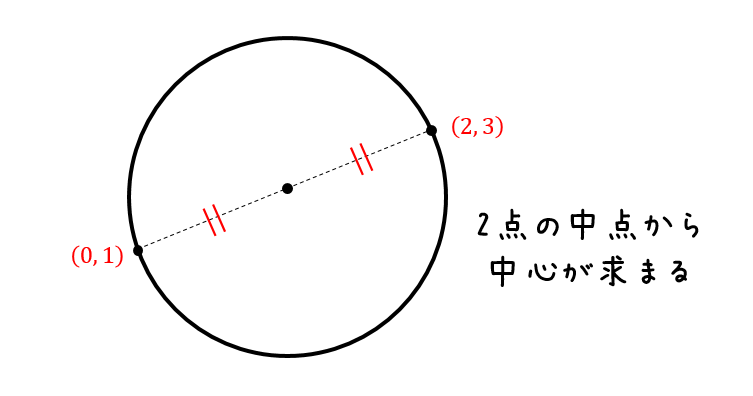



円の方程式の求め方まとめ パターン別に解説するよ 数スタ
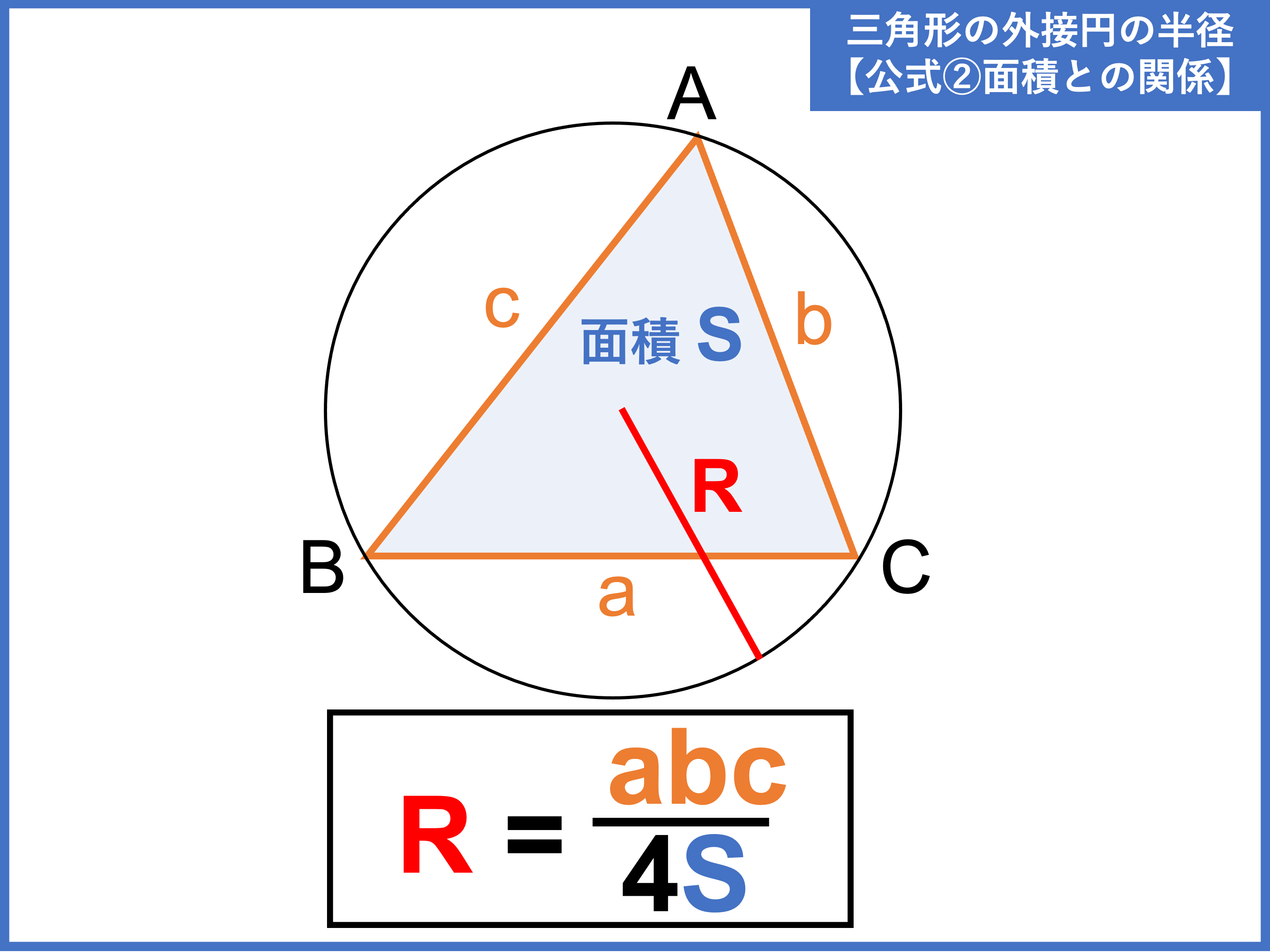



外接円とは 半径の公式や求め方 性質をわかりやすく解説 受験辞典




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




円周の求め方と円の面積について アタリマエ




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
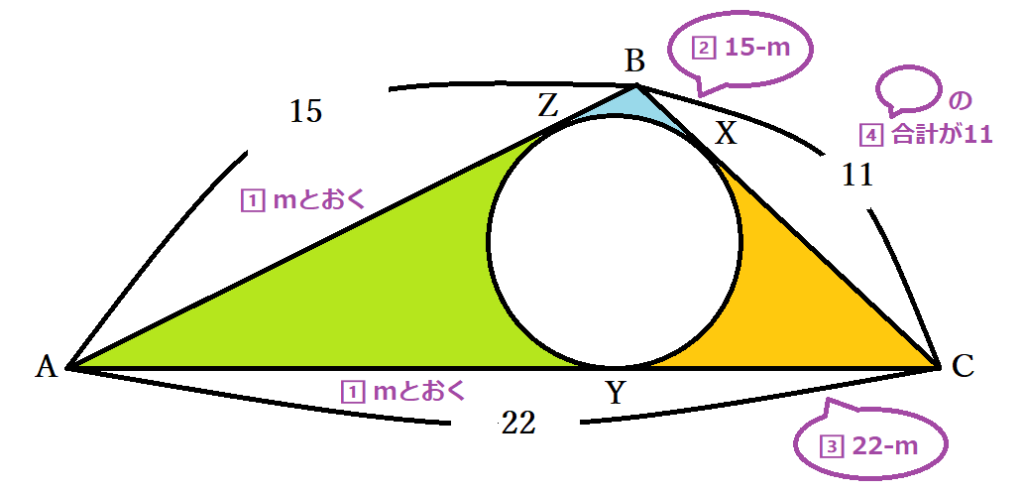



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの学びblog
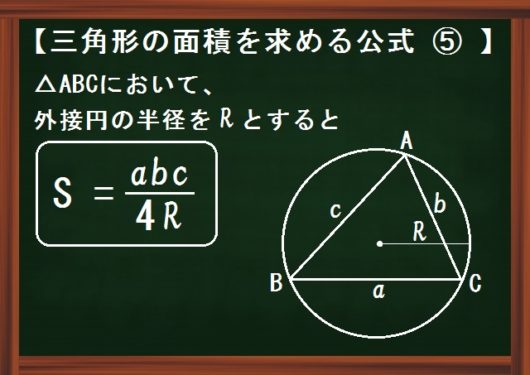



三角形の面積を求める公式7選 高校数学のまとめにどうぞ



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典
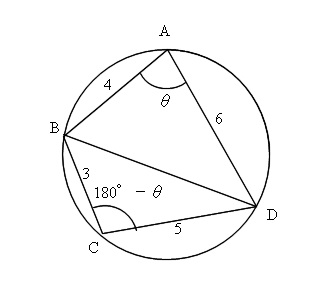



円に内接する四角形の面積の求め方と定理の使い方



0 件のコメント:
コメントを投稿