最小公倍数は168で、この数に3をたした171が答えとなる。 (2) 9で割れば6あまり、6で割れば3あまる整数は3をたせば割りきれる整数 なので、6と9の公倍数に3を引いた整数である。 6と9の最小公倍数は18。18で100に近い整数は108。求める整数は 10=105。 (3)4/8/17 >Q 連続する2つの奇数の和は4の倍数になる。このことを文字を使い説明せよ という問題で私は2n12n1としたんですが、回答には2n12n1となっていました。 2n+12n1ではないのはなぜですか? 2n1が奇数になるのはオッケーだ。1から100までの自然数の和 問題 1234・・・・・・・・ = 5050 の計算を、順々に足していく方法より、楽にできる 方法をできるだけ多く見つけなさい。
Q Tbn And9gctkyehflcixjr9s8zowqnx3q18jipn4abcmkbpzes95k1rvgmrn Usqp Cau
連続する3つの整数の和は3の倍数になるわけを説明しなさい
連続する3つの整数の和は3の倍数になるわけを説明しなさい-5 5つの連続する整数の和が5の倍数になることを次のように説明した。くうらんを埋めなさい。 連続した5つの整数は最も小さい数をnとすると n, ①, ②, ③, n4となる。 その和は n(n1)(n2)(n3)(n4) =5n10 = ④ nは整数なので(n2)も整数となり5(n2)は5の倍数で問13 上の命題が成り立つ理由を説明しなさい. 問14 をアルファベットとする.( ̸= ∅ とする.) はどのような言語か説 明しなさい.( とは異なる!) 問15 以下が成り立つ理由を説明しなさい. 1 ϵ 2



2
具体例で学ぶ数学 > 計算 > 1からnまでの和を求める公式 最終更新日 1 2 3 ⋯ n = 1 2 n ( n 1) 1からnまでの和を求める公式について、具体例と2通りの証明を解説します。和を計算すると (2n1)(2n3) = 4n4 = 4(n1) (3)最後にまとめ。(2)で計算した答が「4の倍数になる」ということを説明する。 ↓ よって2つの連続する奇数の和は4の倍数になる。 説明 nを整数とすると2つの連続する奇数は2n1, 2n3となる これらの和は2/3/18 クラスを3つのグループにわけてみて、どのグループもすべて男性だったとします。 すると、もとのクラスは全員男性、といえますよね。 これと同じことを、整数の世界で考えてみます。 ある整数が3の倍数(3で割り切れるか)を知りたいとします。
②はおかしいよ。右辺を通分すると だから左辺と一致しないだろう。 <先 生> その通り。安易に差の形に分解できるわけではない。②の場合は、さらに分子の3を1に変えるために を掛けておく必要がある。従って、 となる。$816=15$ です。15は3の倍数なので、もとの数 $816$ も3の倍数であることが分かります。 このように、各桁の和を計算することで、 もとの数 $816$ を直接わり算しなくても、 $816$ が3の倍数なのかどうかを、素早く知ることができます。A がベクトルの場合、sum(A) は要素の和を返します。 A が行列の場合、sum(A) は各列の和を含む行ベクトルを返します。 A が多次元配列の場合、sum(A) は、サイズが 1 でない最初の配列次元に対して作用します。 ここでは要素をベクトルとして扱います。この次元は 1 になりますが、他のすべての
連続する整数というのは、 「1と2と3」、「5と6と7」などの 事なのですが、 1ずつ増える数だ と分かれば 話は早いでしょう。 左を「ある数 n」と考えれば、 右は「それより1大きい数」 (n 1) です。 <パターン2> 倍数の問題 2の倍数 → 2 n 3の倍数 → 3 n 9のさけぶ さっきの例題をといていこう! 例題 連続する3つの整数の和が3の倍数になる訳を説明しなさい。連続する3つの整数は n, n1, n2 などで表される。 例 246=12, 468=18 のように連続する3つの偶数の和は 6 で割り切れる」ことの説明の仕方




中学2年生 数学です 説明する問題なのですが どのように書いたらいいのでしょうか Clear




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく
誕生日が一致する確率 誕生日が一致する確率(グラフ) 自分の誕生日と一致する確率 平均値と標準偏差から真の値を推計 サイコロの正確性 視聴率の誤差 じゃんけんで勝負がつく確率 じゃんけんに勝つ方法 ゴルフのハンディの計算 整数の一様乱数の生成等式の変形1 等式の変形2 等式の変形3 等式の変形 (入試問題) 等式の変形 (発展学習) → スg スム版は別包ソス ス ス ス ス スフ撰ソス ス ス ス ス ス ス ス ス ス スニゑソス ス謔ュ スg ス ス ス ス ス ス I ス@ ス ス ス スA ス n ス ス ス スR ス ス スi ス スやる夫 okだお. やらない夫 スペクトルの間隔 をどんなに細かくしていっても,総和のままじゃダメなんだ.周波数が連続化されて,総和が積分になるように話を持っていきたい. やる夫 よく話が見えないお.



Www Tsumugi Ne Jp Member Data Sm3 1 Sm3 1 6 Pdf




中学数学 式による説明 のコツと練習問題
よって4つの連続する奇数の和は8の倍数となる。 説明 nを整数とすると4つの連続する奇数は2n1,2n3,2n5,2n7となる。 これらの和は(2n1)(2n3)(2n5)(2n7)=8n16 =8(n2) nは整数なので(n2)も整数となり8(n2)は8の倍数となる。 よって4つの連続する奇数の和は8のまた各位の数の和は xyzとなる。 その差は (100x10yz)−(xyz) = 99x9y = 9(11xy) x,yが整数なので(11xy)も整数となり、9(11xy)は9の倍数である。 よって3けたの自然数から、各位の数の和を引くと9の倍数になる 整数をnとすると7で割ると3余る数は7n3となる。連続する3つの偶数の和が6の倍数になることを説明しなさい。 4つの連続する奇数の和は8の倍数になることを説明しなさい。 2けたの自然数aがある。この自然数の一の位と十の位の数を入れ替えた数をbとする。 aとbの差が9の倍数になることを式で説明せよ




メルカリ 馬渕教室 システムワーク 中学2年 数学 参考書 780 中古や未使用のフリマ



Http Maekazu Vwgolf Gti Com Print 2 Mojisikiriyo Pdf
3‐連続型確率変数の確率分布 「ある短大の1年生から無作為に選んだ1名の身長」をXcmとする と,Xは連続 Z:サイコロを2回振ったときの目の和の値とするクァンダ(QANDA) 3000万ダウンロードの数学アプリ 今すぐ。 問題。 解決。 全ての問題をクァンダで早く解決しましょう!About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators



連続する3つの整数のうち中央の数をnとすると 残りのふたつの数はそれぞ Yahoo 知恵袋



連続する5つの整数の和は5の倍数になる このわけを説明しなさい もっと Yahoo 知恵袋
素数の2乗差は 5 の倍数, 3 の倍数, 8 の倍数のいずれかである。 5 ( = 3 2 − 2 2), 16 ( = 5 2 − 3 2), 21 ( = 5 2 − 2 2), 24 ( = 7 2 − 5 2), 40 ( = 7 2 − 3 2), 約数の和が素数になる自然数は、 2 と素数かその累乗数の平方数である。しかし、素数やその累乗数の自乗であっ(3)(1)の配列で,7 がいくつあるかを数え,配列の何番目の要素かを表示するプログラムを作成せよ. (4)実数型配列に,数値 102, 98, 33, 84, 119 をscanfを用いてキーボード入力し, 全ての要素の合計と平均を表示するプログラムを作成せよ.先程の例題で2の倍数については考えたので、次の問題として10までの3の倍数の個数について考えよう。 10以下の自然数の集合を u として、そのうち 3の倍数の集合を b とする場合、 b={3, 6 , 9} なので、bの要素の個数は3個なので n(b)=3 である。 さて、



2



数学で連続する3つの偶数の和は6の倍数になることを説明しなさい がわか Yahoo 知恵袋
3つの連続する偶数 の和は 6の倍数になる。 └───────┘ └──┘ └─────┘ A B C Aの部分を文字で表し、計算はB(和)を行い、最後に計算の結果がC(結論)となることを説明する。 Aを文字で表す 3つの連続する偶数は、nを整数として 2n, 2n2, 2n4 とをつくる。このとき,もとの整数と入れかえた整数の和は,11の倍数であることを次のよう に説明した。( )の中に適当な式やことばを入れよ。 説明 もとの数の十の位を a ,一の位を b とすると,もとの整数は( ① ),入れかえた整数は ( ② )で表される。1/6/11 連続する3つの整数を整数nを用いて n-1、n、n+1 と表す。 その和は (n-1)+(n)+(n+1)=3n したがって連続する3つの整数の和は3の倍数になる。 13人




連続する3つの整数の和は3の倍数 もののはじめblog




中学数学 式による説明 のコツと練習問題
5,6,7のように連続する3つの整数どうしの和は、3の倍数になる。3つのうちの1番目の数をnと置き、2番目を n1 、3番目を n 2 と置いてみて、和が必ず3の倍数になることを説明しなさい。② 出る目の和が10の約数になる確率を求めなさい。 ただし,さいころの1から6までのどの目が出ることも同様に確からしいものとする。 (熊本県17年入試問題)をǫδ 論法で厳密に議論するさいには、一様連続性はかかすことができない重要な概念で す。関数の一様連続性に関しては、次の定理が基本的です。 定理4 関数f(x)が有界閉区間I ⊂ R 上で連続ならば、f(x)はI 上一様連続で ある。 3




数学の証明は簡単 解き方を解説しよう 整数編 学習塾 Step By Step




答えを教えてください よろしくお願いします Clear
(3) 3けたの自然数\(m\) の百の位の数字と、一の位の数字を入れかえてできる自然数を\(n\) とします。このとき\(mn\) が99の倍数になることを文字を使って説明してください。 (4) 2,4,6の和は12で、6の倍数になります。このように、3つ続いた偶数の和は6の倍数に関数 y = f(x) の x = a における連続性を調べるには, 関数値 f(a) が存在し,・・・ (2) 極限値 f(x) が存在し,・・・ (3) それらが一致するかどうかで判断します。 2.詳しい方 極限値の存在が微妙な判断となるときは(3)を分けて考えピタゴラス数とは ピタゴラス数とは,直角三角形の3辺の長さとなるような3つの整数の組のことです。 ピタゴラスの定理(三平方の定理)を使うと, a 2 b 2 = c 2 a^2b^2=c^2 a2 b2 = c2 を満たす自然数の組 ( a, b, c) (a,b,c) (a,b,c) をピタゴラス数と呼ぶ。 と




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく



2



Www Saga Ed Jp Kenkyu Kenkyu Chousa H21 04chuu Suu Documents Ikatu Sikinokeisan Sikou Pdf



2



中学2年の数学です5つのつづいた整数のうち 中央の整数をnとし Yahoo 知恵袋




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく




6jue Lhytajpmm




1 1 3 3 Descubre Como Resolverlo En Qanda



Http Www Kyoto Be Ne Jp Gakkyou Cms Action Common Download Main Upload Id 2465




中学数学 文字を使った説明 数樂管理人のブログ




1 1 3 3 Descubre Como Resolverlo En Qanda




中学2年生 数学 文字式の活用 練習問題プリント 無料ダウンロード 印刷 このページの答えのプリント 全部



1




無料 中2数学 標準問題 解答プリント 5 式の計算5 文字式の利用



中2 文字式による説明 の教え方 塾講師 数学マンは踊る




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく




数学 中2 9 文字式の利用 基本編 Youtube



Http Www Kyoto Be Ne Jp Gakkyou Cms Action Common Download Main Upload Id 2841




1 2 2 3 55 Descubre Como Resolverlo En Qanda



Zaitaku Study Net Wp Content Uploads 10 1533f03e08de60cb3ae1 2 Pdf




赤点脱出シリーズ 捨てている人 損です 式による説明問題の解き方 コツさえ分かれば楽勝 夏期講習 生駒市 奈良市の個人契約 家庭教師しゅ 先生




説明 文字式の利用 文字式を使った説明 チビタコのブログ




中2数学の標準問題集プリント よくわかる中学英語 数学の問題プリント




無料 中2数学 標準問題 解答プリント 6 式の計算6 等式の変形
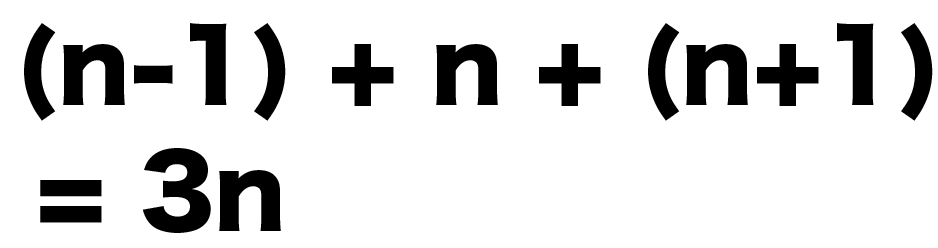



文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく




倍数の個数の求め方 数学 苦手解決q A 進研ゼミ高校講座




メルカリ 別冊解答付き システム数学1問題集 幾何編 代数編 発展編 参考書 800 中古や未使用のフリマ



2




Gwに確認すること 英語 数学編 江戸川台発 勉強がわからない は宝物 小中高生対象の個別指導



Www Mext Go Jp Content 0428 Mxt Kouhou02 Mext 17 Pdf




説明 文字式の利用 文字式を使った説明 チビタコのブログ




連続する3つの奇数の和は3の倍数になることの説明 中学数学 講義 Youtube




Mondai78



2




問題 Aquaアクア



Www Zkai Co Jp Ad Mihon U3tm Pdf



Http Www Saga Ed Jp Kenkyu Kenkyu Chousa H21 04chuu Suu Mondai Sikinokeisan Sikou Pdf Pdf



3つの続いた整数では それら3つの整数の積に中央の整数を加えると 中央の整数の Yahoo 知恵袋




Okra Newmathworkbook Twitter




無料ダウンロード 中2 数学 文字式の利用 問題 中2 数学 文字式の利用 問題



2




中学二三年生 数学 式による説明の準備 1学期中間テスト範囲



Www Pref Oita Jp Uploaded Attachment Pdf



Q Tbn And9gcsj032wcr 6cnslcx5wupxgh7s0hmxa00qycwq7lsonp0ubhpos Usqp Cau




1 1 3 3 Descubre Como Resolverlo En Qanda



Http Mkkc Miyazaki C Ed Jp Research Math Data H27 J Kaitou2 Pdf



連続する3つの整数の和は 3の倍数になる そのわけを説明しなさい と言 Yahoo 知恵袋




ワーク テスト 新しい数学 2年 東京書籍教材編集部 本 通販 Amazon




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく



3 4 5や5 6 7のような奇数から始まる連続する3つの整数の和は6 Yahoo 知恵袋



1



2



Q Tbn And9gctkyehflcixjr9s8zowqnx3q18jipn4abcmkbpzes95k1rvgmrn Usqp Cau



U9j580gf8iba369ji2w Xyz P 2



Www Kyoiku Shuppan Co Jp Textbook Chuu Sugaku Files Ability Survey Task Pdf




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく




連続する3つの整数の和は3の倍数 もののはじめblog



2



連続する4つの整数の和の性質を 文字を使って説明しなさい教えて Yahoo 知恵袋




連続n整数の積は何の倍数 数学の偏差値を上げて合格を目指す



Http Mkkc Miyazaki C Ed Jp Research Math Data H27 J Kaitou2 Pdf



Www City Funabashi Lg Jp Gakkou 0002 Asahi J 0003 P0798 D Fil 4 1 Pdf



2
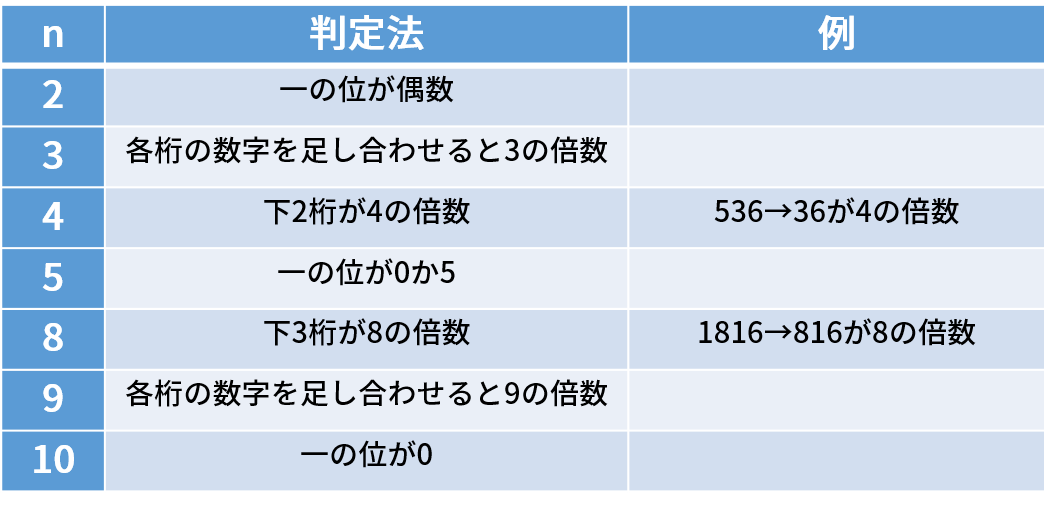



の倍数 を見分ける方法 全部に使える万能なやり方があるのだ



中2数学 標準問題プリント12 式の計算6 等式の変形 問題 6




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく




赤点脱出シリーズ 捨てている人 損です 式による説明問題の解き方 コツさえ分かれば楽勝 夏期講習 生駒市 奈良市の個人契約 家庭教師しゅ 先生




超簡単 式による説明 2 答えの書き方 Shun Ei Note



2



Www Edu City Yokohama Lg Jp School Jhs Hodogaya Index Cfm 1 2658 C Html 2658 0518 Pdf



連続する3つの整数の和は 3の倍数になる そのわけを説明しなさい と言 Yahoo 知恵袋



Http Brewster Jp Text Pdf Newcourse Jrh2 Text Pdf




この問題が分かりません よかったら回答お願いします 問題多くてすみません Clear




これって整数をnとして計算してもいいですか Clear



Http Mkkc Miyazaki C Ed Jp Research Math Data H27 J Kaitou2 Pdf




この問題が分かりません よかったら回答お願いします 問題多くてすみません Clear
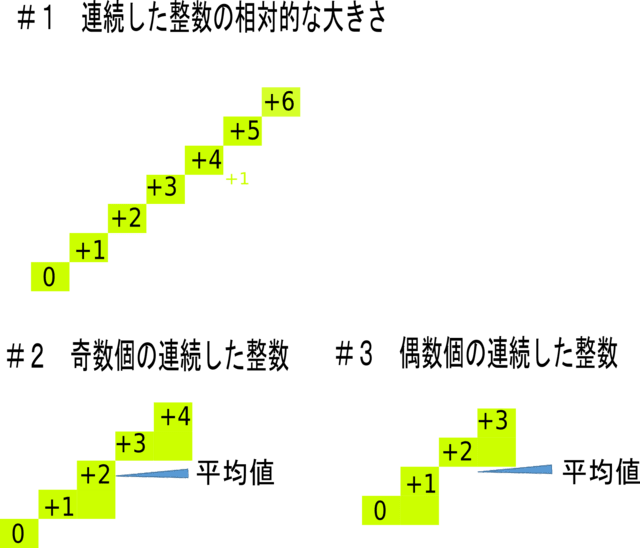



3つの連続した偶数の整数の合計 Sioghesber1



連続する3つの整数の和は3の倍数になるわけを説明しなさい 中学 Yahoo 知恵袋



連続する3つの奇数の和は3の倍数になることを説明せよ と真剣に向き合う 風の貌 かぜのかたち



連続する3つの整数の和は3の倍数になるわけを説明しなさい 中学 Yahoo 知恵袋



Zaitaku Study Net Wp Content Uploads 10 1533f03e08de60cb3ae1 2 Pdf



Core Ac Uk Download Pdf Pdf




中2数学no 16 式の説明 連続する3つの整数の和は3の倍数になる Youtube




中学2年 数学 ハイクラステスト 定期テストや高校入試対策に最適 中学ハイクラステスト Amazon Com Books



Http Www Fdtext Com Dat Suub2 1siki 3ouyou Pdf




1 2 Descubre Como Resolverlo En Qanda




これの 6n 6 6 N 1 というところで なぜ6n 6が6 N Clear




文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく




数学中2授業配信 式による証明5 連問1 Youtube




数字の書かれたカードで整数を作る問題 中学受験算数 カテキョウブログ



0 件のコメント:
コメントを投稿