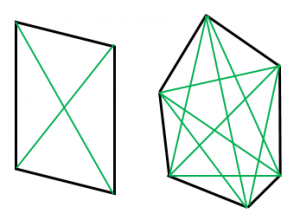
それが9つの頂点分あり、相手側からの物が重複するので2で割ると、 6×9÷2=27 対角線は27本 3つの頂点を結んでできる三角形は 9C3=84個 できる。 正九角形をABCDEFGHIとすると 正三角形は、 頂点を時計回りに2つとばしに選ぶとできる。対角線の交点に関する正18 角形の性質を裏付けるために,対角線の交点の個数を調べてみた。 正n 角形の対角線の交点は,延べ ( 1)( 2)( 3) 24 1 n C4 = n n− n− n− 本 ある。これは,2 本の対角線の両端の4 点を与えれば交点が定まることによる。このうち,実際面白そうなので、もっと他の正多角形についても 調べてみたいというのです。 というわけで正9角形でやってみると やはり真ん中に子供ができています。 (本人の書いた図です) fさんはもっと調べてみたいということで、 どんどん対角線を引いて見ました。

正九角形の対角線 12年 早稲田大 人間科学 数学日和
正9角形 対角線 長さ
正9角形 対角線 長さ- 正方形の対角線の求め方 には公式があるよ。 正方形の1辺をaとすると、対角線は、 √2 a で計算できちゃうんだ。 つまり、 (正方形の対角線)= √2 × (正方形の1辺) ってわけだ。 たとえば、1辺が4cmの正方形ABCDがあったとしよう。 こいつの対角線BDの正十一角形はコンパスと定規だけではもちろん、目盛り付き定規を用いても作図が不可能な図形である。 折り紙でも当然、面積が最大の正十一角形は折れない。 正十一角形の作図 正十一角形は ネウシス作図 (英語版) や2重折り であれば作図可能である。 正十一角形を用いたもの




正多角形の対角線
基本的なので答えのみ. 全3角形数 n C 3 2辺共有 n 1辺だけ共有 n (n4) 3 直角3角形の個数 奇数の場合 0 (∵ 正n角形を真っ2つにする対角線が引けません.) 偶数の場合 対角線 A 0 A n/2 と対角線 A n/2 A 0 が同じですが 1方の領域のみを考える事でダブりを(診 正春数角形の辺、対角線を含めての一筆書きの書き順 け)複雑になりすぎないように偶点である内部の交点は無視して考えることにする。 (イ)右の表のように観則 的に考えるのが1つの 方法である。ただし、 正9角形、正15角形な どのように、頂点 補助線引けば秒殺!正六角形と台形の面積問題~小学生でも解ける問題です 正六角形に図のように対角線を引きました。 元の正六角形の面積は赤色の台形の面積の何倍でしょう? ヒント:頭の中で補助線引いたら秒殺! 解答編補助線・・・
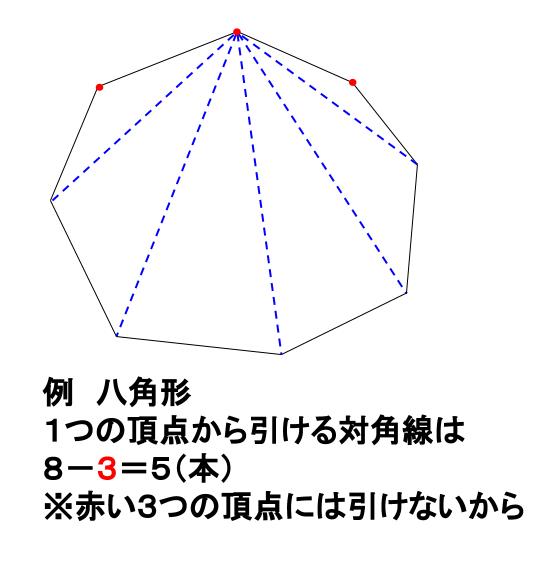
内角 の 和 は1800°、 対角線 の本数は54本である。 正十二角形においては、 中心角 と 外角 は30 ° で、内角は150°となる。十角形の場合,一つの頂点から引ける対角線の本数は 10-3=7(本). 自分自身と両隣には対角線を引けませんが,それ以外の7つの頂点には対角線を引ける. 頂点は全部で10個あるので,7x10=70(本). ただし,それだと同じ対角線を二度ずつ数えて正素数角形の任意の3 本の対角線は 頂点以外の1 点で交わらない 問題1 複素平面上の2 点α1,α2 を通る直線の方程式を求めよ. 解 z ¡α1 α2 ¡α1 は実数なので z ¡α1 α2 ¡α1 z ¡α1 α2 ¡α1 整理して (α2 ¡α1)(z ¡α1) = (α2 ¡α1)(z ¡α1)(α2 ¡α1)z ¡α1α2 α1α1 = (α2 ¡α1)z ¡α1α2 α1α1(α2 ¡α1)z ¡α1α2 = (α2
正多角形の場合の数 正多角形の対角線の数、正多角形の頂点で作る三角形についての場合の数を考えます。 正八角形ぐらいまでなら手書きで考えられるかもしれませんが、それ以上になると手書きでは難しいと思います。 一般化して正n角形で考えてみる 一辺の長さから対角線の長さを求める 例題1 まずは、正方形1辺の長さから対角線の長さを計算する問題について、考えていきます。 ここで、辺の長さを3cmとして、その対角線の長さを求めてみましょう。 解答1正7角形の対角線の長さに関する問題で 1/x1/yを求めていますが その逆数を求めると単位の次元が合うのでおもしろいかなとおもいました。 1/(1/x1/y)=a となり(a=正7角形の1辺の長さとする)すると次のように表現できる。




正多角形の対角線の交点 数学 オリジナル問題 7 Youtube




Inkscape 正多角形対角線を引いてみた パソコン備忘録
2個の頂点を結ぶ線分の本数 6c2=15 本から、辺の数を引いたら、対角線の本数が出ます。(156=9 ) 答えは、9本 間違えていたら、ごめんなさい!2.正12 角形の対角線の性質について調べてみよう。 3 本以上の対角線が交わって いる点は図のように3 種類に分 類できる。 緑の点 赤の点 青の点 このうち、青の点で3 本の対角 線が交わることを説明してみよ う。 〔ヒント〕 正12 角形の辺ac に対する中正7角形の辺の長さを 2 +c 2 /b 2 +a 2 /c 2 の値を求めよ。 2式から代数の問題として解いてもいいし、正7角形の辺と対角線であることから三角関 数とかを使ってもかまいません。




正九角形の対角線 12年 早稲田大 人間科学 数学日和




正多角形 Wikiwand
正n角形の対角線の数を求める公式を次の1から3の手順で導け。ただし、nは4以上の整数とする。 1正n角形のn個の頂点の中から2個を選ぶ選び方の総数を求める 2隣り合う2つの頂点を選ぶときの選び方の総数を求める 3①で求めた総数をひく 大至急お願いいたしますm(__)m 正多角形をすべての対角線で分けた二等辺三角形の面積を求めて、その和を求める方法もあるので、上記の公式を無理して覚える必要はありません。 (二等辺三角形に分ける方法については、計算問題①で解説します!) 正 n 角形の面積の公式(n = 3, 4, 5, 6)正5角形 1辺の長さが1の正5角形の対角線の長さは になっています.ユークリッド(紀元前300年)は,これに基づいて,正5角形の作図法を与えました. 紙テープ(や割り箸の袋)を結んでうまく折ると,結び目に正5角形が現れます.



1



多角形の対角線の本数を求める公式 具体例で学ぶ数学
図形の性質の調べ方 平行線と角(3) 1 次の図で、l mのとき、∠x、∠yの大きさを求めなさい。同じ印をつけた角は それぞれ等しい。 (1) (2) (3) 243 x 70° 115° E x l 40° m x l ° m x l 10° m(4) 正12 角形の対角線の交点のうち,頂点を除く個数を求めよ。 (解)正12 角形以降からは,中心を通らない 対角線同士でも交点ができるところに注意。 2 本の対角線の交点の個数 228(個) 3 本の対角線の交点の個数 60(個)凸n 角形(の辺および対角線)を m 角形(の辺あるいは対角線)で取りつくすという問題 定理1 凸n 角形の頂点を結んでできる線分,つまり辺または対角線はnC2 = 1 2 n(n¡1) 本である. 証明略 定理2 凸n 角形の頂点を結んでできる凸m 角形はnCm 個である. 証明略 例えば正n 角形などの場合,合同




対角線とは 多角形の対角線の本数の2通りの求め方 算数パラダイス



正多角形2
正奇数角形の場合は、 n C 4 (個) 正偶数角形の場合は、 n C 4 -Σk=3~?{(k C 2 -1)・a k} のような形で書けるのではないかと予想された。 凡人さんは、現在、次の問題点を研究中とのこと。 ・正奇数角形であれば、3本の対角線が1点で交わることが無いのか?正五角形を(定規とコンパスのみを使って)作図する方法を解説します。 正五角形の作図の原理を理解するために,まずは1辺が1の正五角形の対角線の長さについて考えます。 とにかく作図方法だけ知りたい! という方はページ下部のグレー背景部分(2正n角形の対角線はn (n3)/2本ありますが、これらの交点は何個あるのか、気になります。 ここで難しいのは、異なる3本の対角線が一点で交わることがありうるからです。 さらに、異なる4本の対角線が一点で交わることもあったりして複雑なかんじがします



数aの問題がわかりません 正九角形の3つの頂点を結んでできる三角形 Yahoo 知恵袋




頂点間の長さの種類の個数を求める問題 17年 広尾学園中学校 恋する中学受験 大学受験を見据えた中学受験
正多面体 プラトンの正多面体とも呼ばれる. 同じ大きさの正多角形(正p角形)で囲まれ、 どの頂点にも同数個(q個)の正多角形が集まって、 同じ形をしている立体を正多面体という. このときp≧3, q≧3 である. (p, q) をシュレーフリーの記号という.正5角形・正7角形とトレミーの定理(その3) 正多角形 Wikipedia;Q正n角形が半径1の円に内接している.すべての辺(n本)と対角線(n(n-3)/2本),合計n(n-1)/2本の長さの平方和(sum of squares)を求めよ. n(n+2)-2n=n^2 1nが奇数のと



正九角形の3つの頂点を結んでできる三角形のうちで 正九角形と辺を共有しない三角 Yahoo 知恵袋




192 正9角形の辺と対角線でできる の個数は アットランダム ブリコラージュ 転ぶな 風邪ひくな 義理を欠け 長寿の心得 岸信介 食う 寝る 出す 風呂 在宅生活4つの柱
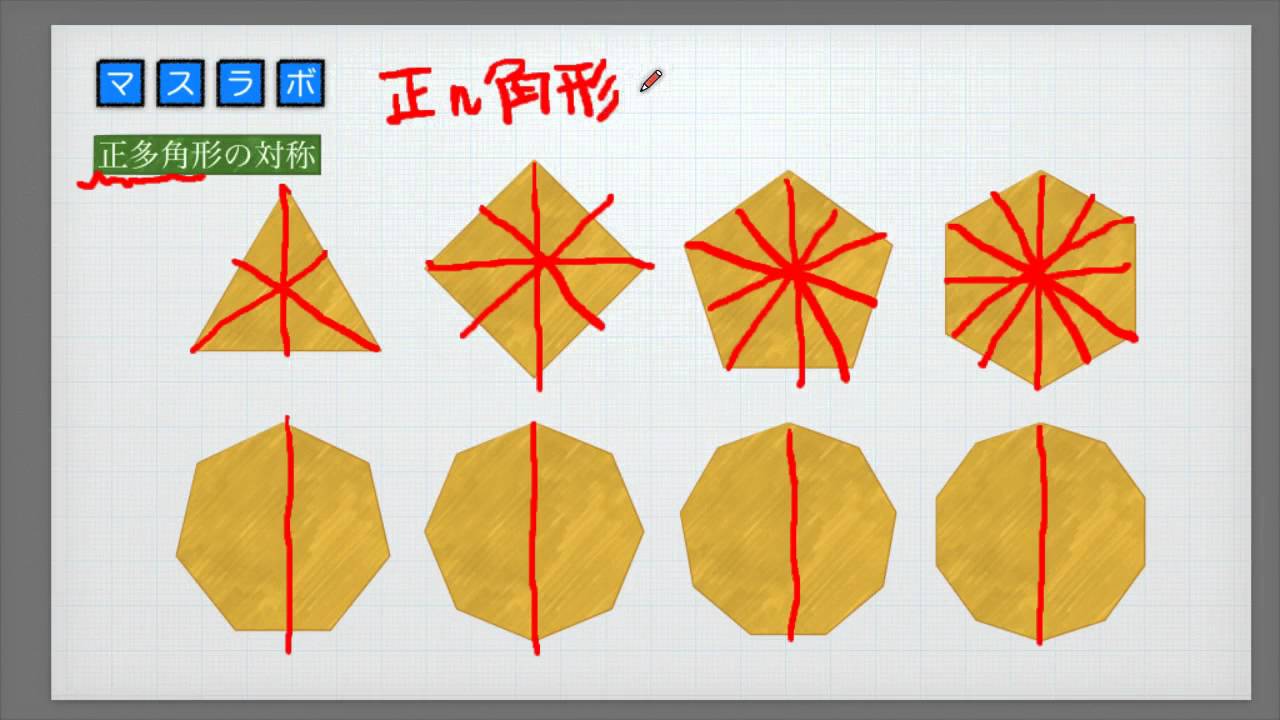
正多角形の例 一般に、正 n 角形は全て線対称で、対称の軸は n 本あります。 というのは確認しました。 なども成立します。 理由を簡単に説明してみます。 n が奇数のときは、頂点と対辺の中点を通る直線(全部で n 本ある)が対称の軸です。 それ正方形の対角線の求め方は「一辺の長さ×√2」です。 一辺の長さが10cmの正方形の対角線の長さは「10cm×√2=10√2cm」です。 √2≒141なので、10√2≒141cmになります。 なぜ「一辺の長さの√2倍」になるかは、ピタゴラスの定理を用いて説明できます。 子供の中学校時の作品(多角形対角線)を Inkscape でまねてみました。 正多角形対角線図を描く 1.正多角形を描く 画面左側の「ツールボックス」から「星形/多角形ツール」を選び、19角形を描く (ガイド線を入れているがガイド線は特に必要では



Idan Tal
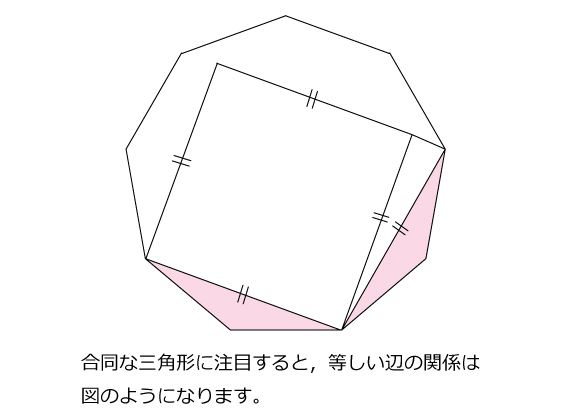



図形ドリル 第11問 正九角形と正方形 算数星人のweb問題集 中学受験算数の問題に挑戦
正十角形 対角線 (10−3)×10÷2=35で、正十角形の対角線の本数は35本ということがわかります。 このように、正n角形の対角線の本数は(n−3)×n÷2で出すことができるのです。 ぜひ覚えておいてくださいね。 正八角形について、次のものの個数を求めよ。 (1)対角線 ヒント:正n角形において (辺の数)(対角線の数)=nC2 (1)対角線および辺の数=8C2=28(本) 辺の数は8本。正九角形 正九角形においては、中心角と外角は40 °で、内角は140°となる。 一辺の長さがaの正九角形の面積Sは、 = となる。 (/) を平方根と立方根で表すと 、 = = = = = 正九角形は定規とコンパスによる作図が不可能な図形である。 正九角形の頂点を二つおきに線で結ぶと正三角形が




七角形 Wikipedia



正多角形2
:正7角形の交わらない対角線による 分割 :4^101は3で何回割れる? : abc内の点o, oab, obc, ocaの外接円の半径が等しい時のその半径は? スポンサーサイト正 7 角形 対角線 正十角形の対角線は何本ありますか?説明つきでお願いします 正7角形のある性質 xsrvjp;
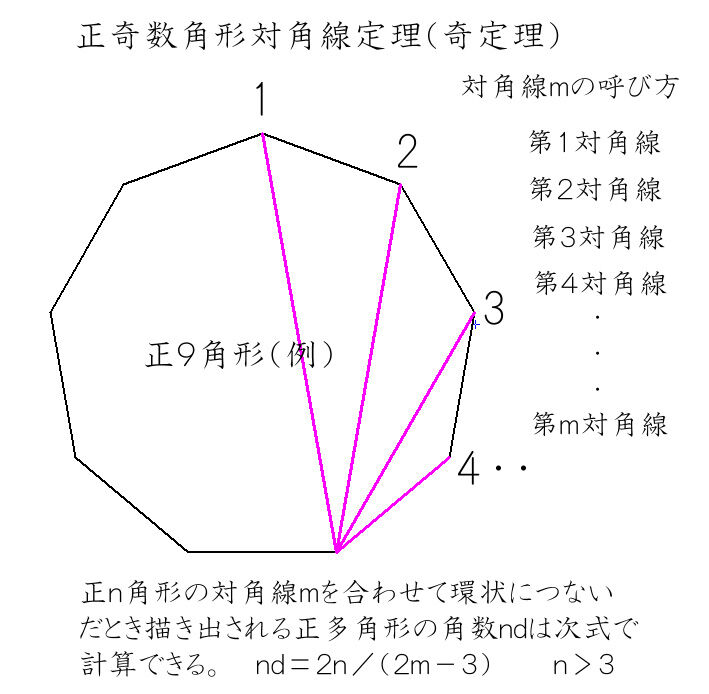



正多角形作図自由自在 正多角形第2定理 正多角形対角線定理 発想力教育研究所 素数誕生のメカニズム
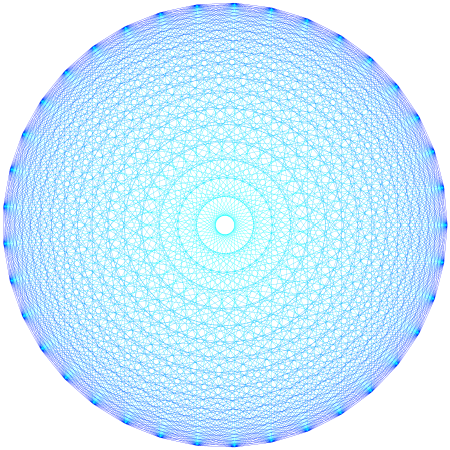



正多角形の対角線



平面図形の角度 第42問 正九角形 北嶺中学 05年 学習院女子中等科 10年 入試問題 算数 まいにち一題 中学受験過去問題研究
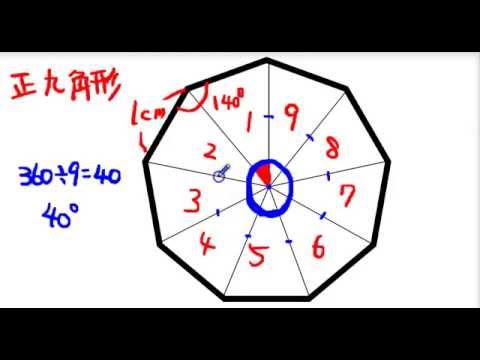



正多角形の性質 正九角形を例に Youtube




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく



1
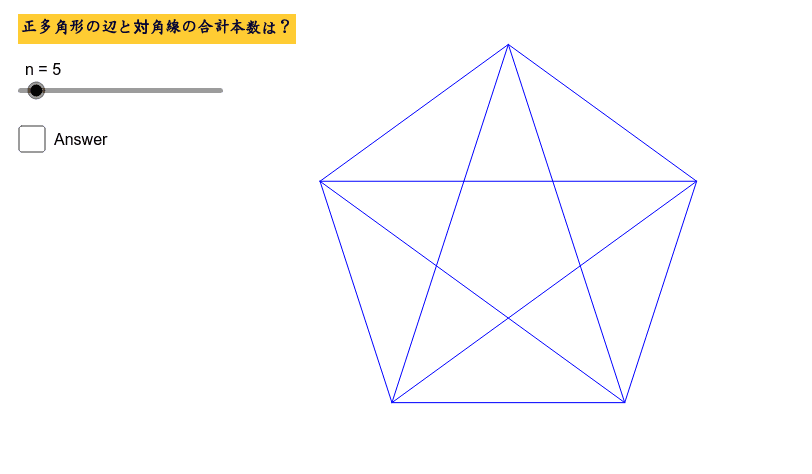



正多角形の辺 対角線の本数 Geogebra




9角形と太った9芒星 コスモス
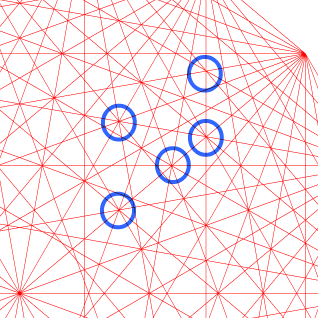



正多角形の対角線



Metatronic Metalogue 114




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より



数学aの問題教えて下さい正九角形がある対角線の本数は 3つの頂点を結ん Yahoo 知恵袋



実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note




図形 奇数の正多角形の直径算出 奇数の正多角形 三角 五角 七角 数学 教えて Goo



正多角形の辺と対角線




九角形 Wikipedia



実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note




Vers Le Haut 正12角形 書き方 正12角形 書き方



09年6月6日の 正九角形の対角線の問題 のヒント



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



その1 驚き 正n角形の1頂点から他の頂点までの全線分の積はn



いろいろな正多角形をかいてみよう 家庭学習レシピ



正多角形の内接円の半径 倭算数理研究所




正九角形の対角線の交点の数を求める 中学受験プロ講師ブログ




正多角形の面積 倭算数理研究所



1




正多角形の対角線 あなたと夜と数学と




九角形 Wikipedia



正九角形の対角線の交点の数を求める 中学受験プロ講師ブログ




正多角形の対角線



正九角形は一筆書きでかかけますか 奇数だと一筆書きができるようなことを Yahoo 知恵袋




正九角形の対角線の交点の数を求める 中学受験プロ講師ブログ



たのしい算数 正多角形はキレイだからこそ キッズライト 公式サイト 福岡 西都小学校前の学童保育 学習塾 四谷大塚net 東進こども英語塾




正八角形の対角線の本数 おときち副塾長 電脳空間学習塾かもん Youtube



お久しぶりです 中学受験算数角度正多角形で対角線をひくと 角度は Yahoo 知恵袋



小学校6年生 算数 正多角形の対称 Youtube



算数にチャレンジ



その1 驚き 正n角形の1頂点から他の頂点までの全線分の積はn



多角形 中学受験 の問題31題をただひたすら解くページ チャンプルー




正多角形の対角線の長さ 香料ゐっすゐの夢




Wolfram Alpha Japan 正多角形の名前を入れると 内角や内角の和 対角線の数など いろいろな関連情報が出てきます すべての頂点を線で結ぶと きれいな模様になりますよ T Co Gs8vlxiijm Wolframalpha 幾何学 正多角形 内角 T Co



中学数学 多角形の対角線の本数 中学数学の無料オンライン学習サイトchu Su




七角形 Wikiwand




九角形 Wikiwand




小5 算数 小5 54 正多角形 Youtube




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく




正多角形の対角線



対角線の数って どうやって計算するんだ 名寄 算数数学教室より



多角形の対角線の本数を求める公式 具体例で学ぶ数学




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく




正多角形の対角線 あなたと夜と数学と




高校数学 正多角形の面積の求め方 映像授業のtry It トライイット



1




正多角形の対角線の長さの種類 香料ゐっすゐの夢



小学生の息子の宿題です 解説をお願いします 正9角形のとき イの角度 Yahoo 知恵袋



Idan Tal




おぉ 寒い寒い 正多角形の対角線



正多角形 算数用語集




多角形の対角線の作図は正確に書けると子供達は必ずはまります この喜びが子供を育ててくれます 七田式天六教室 本町教室及び魔法の折り紙オンライン教室は算数 数学のスペシャリストを育てます




正多角形の対角線 あなたと夜と数学と




正多角形の対角線




小学校5年 算数 正多角形の角の大きさ Youtube
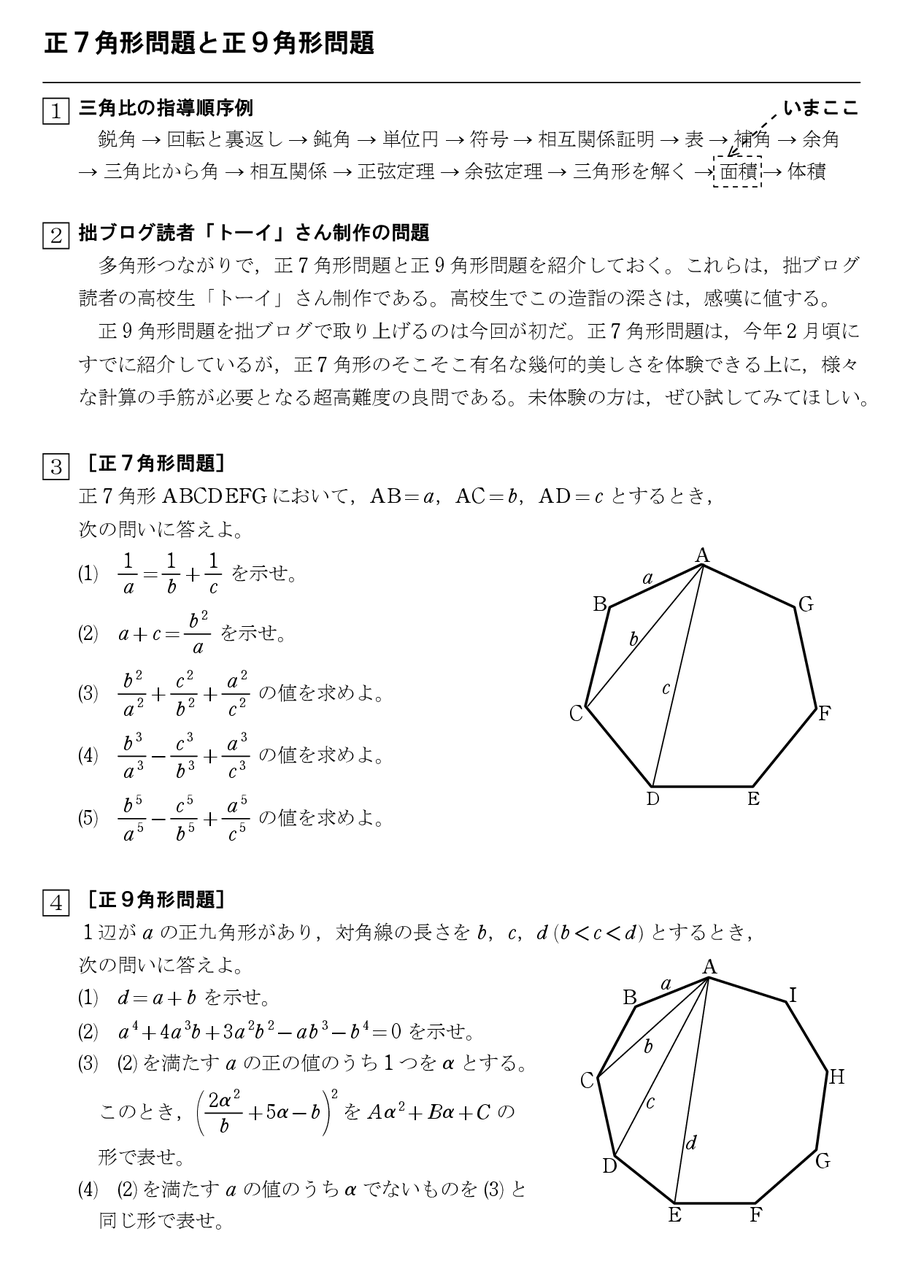



正7角形問題と正9角形問題 怜悧玲瓏 高校数学を天空から俯瞰する
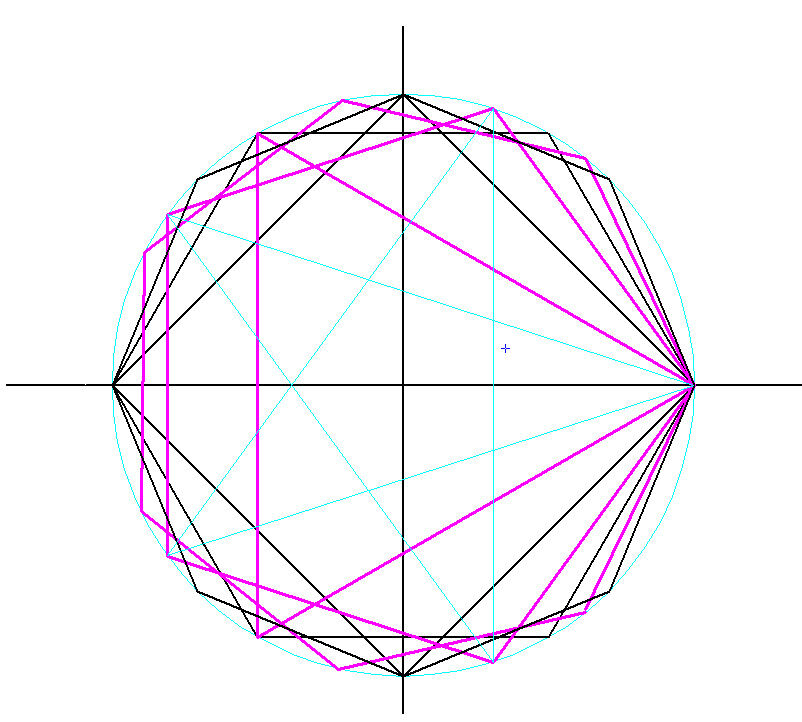



正多角形の角数 偶数奇数 と人類の至宝e Ip ー1の幾何学的関係 発想力教育研究所 素数誕生のメカニズム




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




十角形 Wikipedia




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく




多角形の英語 五角形 六角形 八角形 12角形 正多角形など 英語独学マスター




ポテト一郎 正七角形 正七角形の美しい性質を見つけました 赤の面積は青の面積の2倍になっています




対角線とは 多角形の対角線の本数の2通りの求め方 算数パラダイス



正多角形2



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス




高校数学a 正多角形内の三角形の個数 二等辺三角形 正三角形 直角三角形 鈍角三角形 鋭角三角形他 受験の月



対角線を描く すぐる学習会




六万五千五百三十七角形 Wikipedia




鏡で正多角形 あなたと夜と数学と




単位円に内接する正n角形の1つの頂点から他の頂点にひいた線分の積 数学の偏差値を上げて合格を目指す



正17角形と正18角形




正多角形および星形一筆書と素数判定法 ベータ版 茜町books
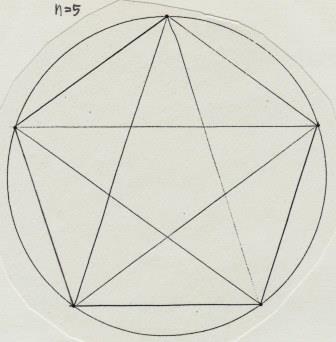



正多角形の対角線 あなたと夜と数学と



図形 正十二角形の分解 父ちゃんが教えたるっ
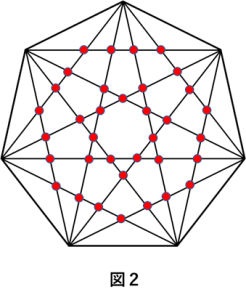



正九角形の対角線の交点の数を求める 中学受験プロ講師ブログ




いろいろな正多角形をかいてみよう 家庭学習レシピ
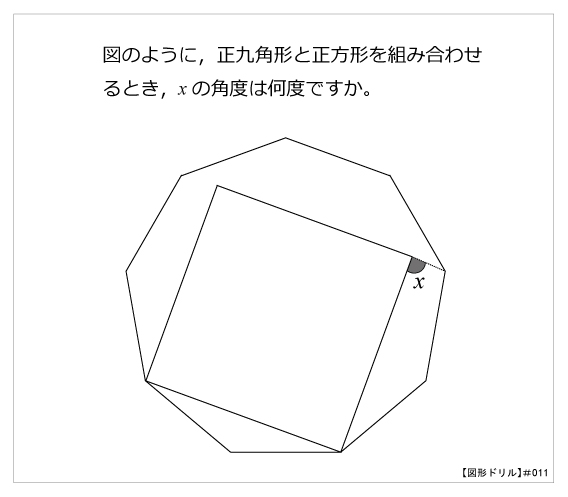



図形ドリル 第11問 正九角形と正方形 算数星人のweb問題集 中学受験算数の問題に挑戦




1 1 Lihat Cara Penyelesaian Di Qanda




正多角形 Wikipedia



早稲田大学 人間科学学部 文系 12年問題4 Suugaku Jp




角形の対角線の本数問題 18年 横浜市立南高等学校附属中学校 恋する中高一貫校 適性検査 徹底攻略



0 件のコメント:
コメントを投稿